Робастные системы и адаптивное управление

         Тема 7.   Робастные системы и адаптивное управление

Для любого объекта управления может быть построено и разработано неограниченное количество алгоритмов управления. Количество алгоритмов зависит в первую очередь от уровня знаний об объекте, от полноты априорной информации сложности объекта, от технических требований к созданию алгоритмов и от интуиции инженера, проектирующего АСУ ТП.

Подавляющее большинство технологических процессов в нефтепереработке и нефтехимии содержат аппараты или узлы, обладающие стареющими характеристиками, которые приводят к дрейфу оптимальных режимов. Это приводит к неизбежности периодического поиска оптимального режима и свидетельствует о том, что стабилизация технологических параметров не обеспечивают максимальной эффективности управления. Поэтому основной путь к повышению эффективности производства лежит через применение АСУ ТП и количественно обоснованный синтез алгоритмов управления для управляющей подсистемы АСУ ТП.

Вследствие своих внутренних специфических особенностей оптимальный режим технологического процесса случайным образом перемещается в пространстве состояний (дрейфует). Причинами дрейфа являются износ оборудования, старение катализатора, износ инструмента и т.п.

В условиях непрерывного дрейфа характеристик объекта алгоритм  управления должен быть построен так, чтобы на основе измерения текущих входных и выходных параметров процесса постоянно корректировалось значение основных управляющих воздействий, т.е. в алгоритме управления, естественно, должна максимально возможно использоваться априорная информация об объекте, если таковая имеется. Возможны случаи, когда в алгоритме управления используется только часть априорной информации, позволяющей оценить ситуацию в объекте.Всё это даёт основания классифицировать робастные систем по объёмам использования текущей и априорной информации в них.

 

Рисунок 7.1      Классификация робастных систем

Робастные системы управления можно разбить на три типа, характеризующиеся различным соотношением использования  в них текущей и априорной информации:

1. безмодельные робастные системы; они основаны на обработке данных нормального функционирования объекта, т.е. используют только текущую информацию и позволяют по данным обработки текущей информации определить положение экстремума критерия управления; процесс определения положения рабочей точки при этом называют процессом текущей идентификации(см.слайд 76);

2. Робастные системы с эталонной моделью используют всю текущую информацию для идентификации свойств эталонной модели; априорная информацию сосредоточена, при этом, в упрощённой эталонной математической модели объекта управления, которая используется для поиска оптимальных режимов функционирования этого объекта управления;

3. Комбинированные робастные системы используют всю текущую информацию об объекте и всю априорную информацию в виде полной эталонной модели объекта управления. Основным отличием комбинированных робастных систем является применение в них  безмодельной идентификации положения рабочей точки.

Широко распространена классификация робастных систем по способу реализации оптимального управляющего воздействия. Здесь различают супервизорное управление, когда линия подачи управляющего воздействия разорвана (см. рис.7.1) и адаптивное управление, когда линия подачи управляющего воздействия замкнута.

7.1 Безмодельные робастные системы

Наиболее широкое применение, в промышленных системах, нашли безмодельные робастные системы. Алгоритмы управления, в них, основаны на данных нормального функционирования и не требуют больших знаний о свойствах объекта управления.Все нужные знания об объекте формируются алгоритмом  в результате процедур идентификации.

Одним из распространенных методов идентификации в безмодельных робастных системах является метод наименьших квадратов, который  позволяет идентифицировать положение рабочей точки объекта управления по данным нормальной эксплуатации, использовав при этом среднеквадратический критерий качества. Метод заключается в требовании наилучшего согласования выбранной зависимости и экспериментальных точек так, чтобы сумма квадратов отклонений экспериментальных точек от выбранной аппроксимирующей зависимости обращалась в минимум:

                                      

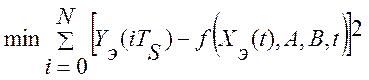
где  Y_э(iT_S) – наблюдаемые экспериментальные точки;  – аппроксимирующая зависимость или модель рабочей точки объекта управления.