Робастные системы и адаптивное управление, страница 3

1.    Достоверность оценки величины производной  зависят не столько от сложности объекта управления, сколько от точности и чувствительности применяемых технических средств измерения.

2. На первый план выдвигается разработка алгоритмов визуализации процессов измерения и управления;

3. Основной проблемой является количественно обоснованный выбор критериев эффективности работы энергооборудования.

Пример 11.1. Система оптимального управления процессом производства эндогаза (см. рис. 7.4.) . Поставлена задача, управлять эндогазогенератором по эффективности его функционирования, Y₂(t).  Основным возмущающим параметром критерия управления является температура в реторте, Y₁(t), которая управляема при помощи расхода газа, X₁(t). Качество целевого продукта (эндогаза) регулируется расходом воздуха, X₂(t). Предпроектные исследования показали, что критерием управления целесообразно взять эффективность работы эндогазогенератора:

  .                     

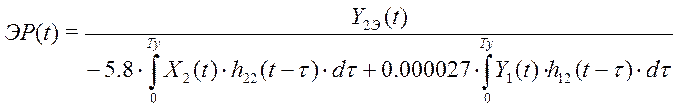В дискретном виде критерий управления записывается следующим образом:

,           

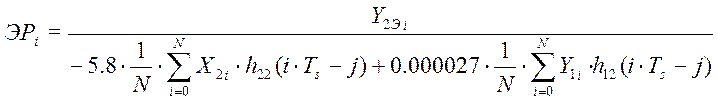где T_s– период опроса датчиков,  N– длина массива данных.          Имитационное моделирование процессов управления показало, что зависимость погрешности обработки измерительной информации по выбранному критерию имеет экстремальный характер (см. рис. 7.5.).

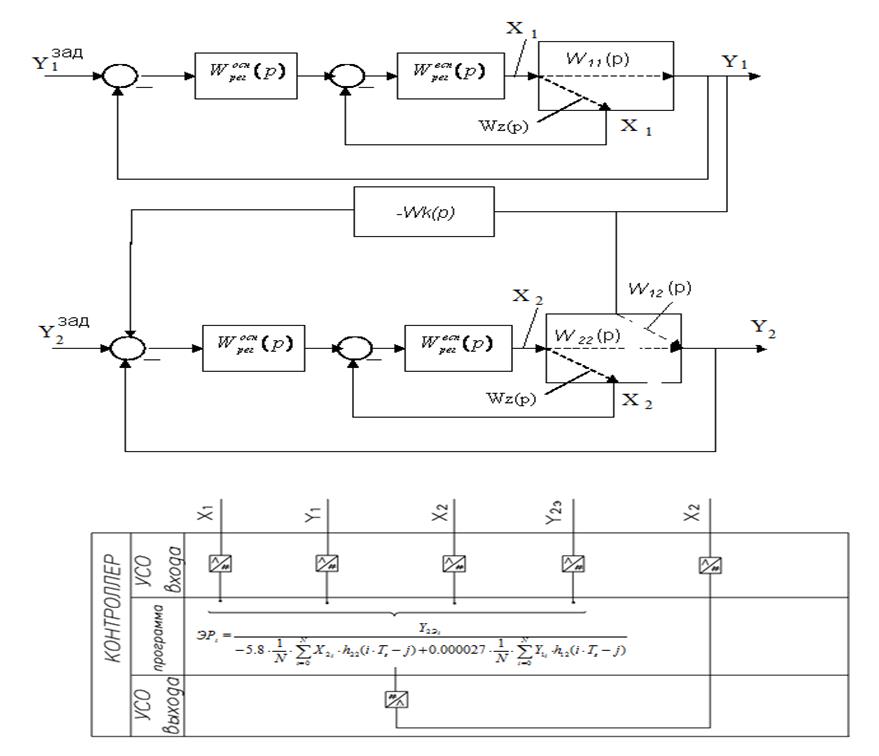
Рис. 7.4. Система оптимального управления эндогазогенератором

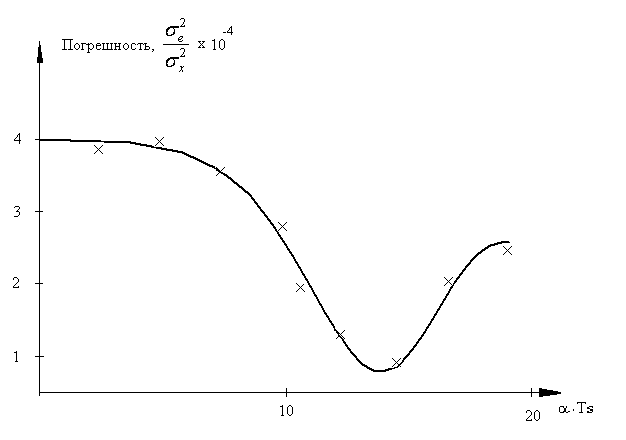
Рис. 7.5. Оптимальные настройки системы         

7.2. Робастные системы с эталонной моделью

Робастные системы с эталонной модельюимеют так же большое применение при управлении техническими системами. Существует большая группа алгоритмов, принцип построения которых основан на применении математической модели процесса (аппарата). Особенностью таких алгоритмов является использование всей текущей и части априорной информации, которая сосредоточена в упрощенной эталонной модели объекта управления. Анализ алгоритмов управления, методов их синтеза, а также методов идентификации позволяет представить структуру робастной системы с эталонной моделью в виде (см. рис. 7.6).

 

 – вектор входных параметров;  – вектор выходных параметров;  – вектор параметров, подлежащих идентификации;  – вектор оптимальных значений управляющего воздействия.

Рис. 7.6.  К понятию робастной системы с эталонной моделью.

На первом этапе (процедура идентификации) (см. рис. 7.6).  функционирования алгоритма решается оптимизационная задача:

                                                     ,                                                            

где   – вектор дрейфующих параметров эталонной модели, подлежащих идентификации;        – функционал невязки между экспериментальными и рассчитанными по эталонной модели значениями выходных параметров; –область допустимых решений (выбирается из априорных знаний об объекте управления).  Текущая информация, в таких алгоритмах управления, используется для идентификации неизвестных параметров, заложенных в математическую модель как неизвестные константы. Как правило, метод идентификации, при этом, относится к классу задач квадратического программирования (например, метод наименьших квадратов).  

На втором шаге (процедура оптимизации) (см. рис. 7.6) априорная информация  формализована в виде математической модели и используется для отыскания оптимального режима и принятия решения по управлению процессом (см. рис. 7.6). При этом решается оптимизационная задача вида:

 

                                                   ,                                                    

где   – оптимальные значения управляющих параметров;  – эталонная математическая модель объекта управления; V- область допустимых значений управляющего воздействия.

Метод оптимизации, при этом, выбирается с учётом  особенностей критерия управления (эталонной модели объекта):