2. Комбинированные алгоритмы используют модели объекта управления в виде совокупности статических и динамических характеристик, что позволяет идентифицировать не только направление дрейфа критерия управления, но и уменьшить потери информации.
3. Они позволяют оптимизировать величину шага движения к оптимальному значению управляющего воздействия.
4. Наиболее целесообразно применять комбинированный алгоритм в условиях больших флуктуаций входных параметров, а также в условиях большой инерционности объекта управления.
5. Комбинированные алгоритмы позволяют отслеживать дрейф оптимального режима и вырабатывать управляющее воздействие, компенсирующее этот дрейф. В отличие от алгоритма первого типа комбинированные алгоритмы точнее и надежнее.
ПРОБЛЕМЫ:
1. Достоверность показаний виртуальных приборов комбинированных робастных систем зависит не столько от сложности математической модели объекта управления, сколько от точности и чувствительности применяемых технических средств измерения. Под показаниями виртуального прибора понимается решение упрощенной эталонной модели объекта управления.
2. При этом на первый план выдвигаются, упрощение полной эталонной модели до «возможностей системы» и возможностей алгоритмов визуализации процессов измерения и управления.
3. проблемой является количественно обоснованный выбор критериев управления и диагностика эффективности работы энергооборудования.
Пример 11.3. Комбинированная робастная система управления процессом непрерывного розлива стали. Анализ технологического процесса непрерывного розлива стали показал, что для повышения качества продукции необходимо поддерживать постоянным уровень металла, H(t), в кристаллизаторе, который способствует уменьшению количества неметаллических примесей и провалов металла под кристаллизатором. Уровень металла в кристаллизаторе может поддерживаться с помощью двух основных регулируемых параметров – это скорости вытяжки, V(t), заготовки из кристаллизатора и расход металла, G(t), в кристаллизатор. Температурный профиль по высоте кристаллизатора регулируется системой охлаждения, для оптимального функционирования которой необходим прогноз температуры внутренней стенки кристаллизатора. Для этих целей и предлагается математическая модель, адекватность которой подтверждена данными пассивного эксперимента, полученными на реальном объекте управления.
За эталонную
модель профиля температур по габаритным размерам кристаллизатора ![]() вязкого жидкого металла, движущегося
внутри кристаллизатора со скоростью
вязкого жидкого металла, движущегося
внутри кристаллизатора со скоростью ![]() =
=![]()
![]() ,
,![]() ,
,![]()
![]() . Где
. Где ![]() ,
, ![]() ,
, ![]() принято
уравнение теплопроводности:
принято
уравнение теплопроводности:
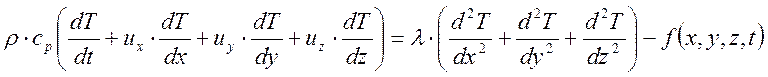 ,
(1)
,
(1)
где ![]() - плотность расплава;
- плотность расплава; ![]() - удельная теплоёмкость металла;
- удельная теплоёмкость металла; ![]() - коэффициент теплопроводности [1]. Пусть геометрические
параметры кристаллизатора имеют вид:
- коэффициент теплопроводности [1]. Пусть геометрические
параметры кристаллизатора имеют вид:
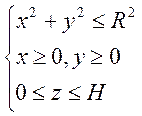 ,
,
Для целей управления целесообразно использовать математическое описание процесса конвективного теплообмена, которое состоит из уравнения неразрывности (2) и трех уравнений движения по пространственным координатам (3 -:- 6). В частности, для потока несжимаемого жидкого металла, при условии, что вязкая диссипация (рассеяние) энергии пренебрежимо мала, эти уравнения имеют вид:
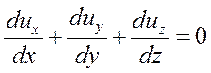 ;
(2)
;
(2)
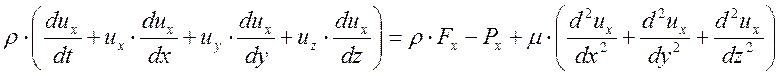 ; (3)
; (3)
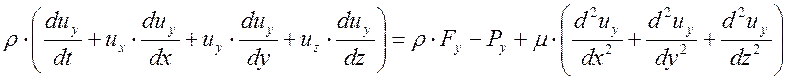 ; (4)
; (4)
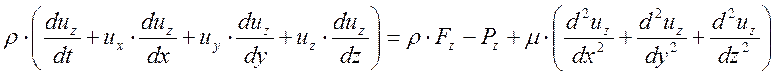 , (5) где
, (5) где ![]() -
компоненты массовых сил;
-
компоненты массовых сил; ![]() - компоненты поверхностных
сил;
- компоненты поверхностных
сил; ![]() - плотность;
- плотность; ![]() -
коэффициент динамической
вязкости.
-
коэффициент динамической
вязкости.
Если
составляющие функции скорости определить как:![]()
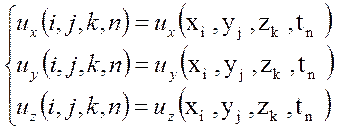 ,
(6)
,
(6)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.