Робастные системы и адаптивное управление, страница 2

Метод наименьших квадратов имеет существенные преимущества перед другими методами: во-первых, он приводит к сравнительно простому алгоритму идентификации; во-вторых, позволяет дать этому  алгоритму идентификации теоретическое обоснование с вероятностной точки зрения. Алгоритм идентификации получается путем дифференцирования и приравнивания к нулю первых производных по идентифицируемым параметрам. Так как в окрестности рабочей точки статическая характеристика объекта управления линеаризуема в малом, то модель рабочей точки  объекта управления может быть выбрана в виде линейной функции: . Тогда, дифференцирование критерия управления  по А и В дает:

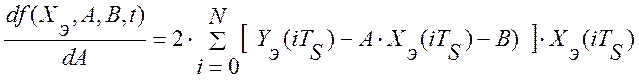
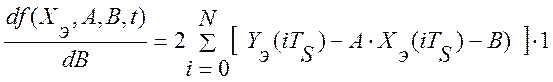
Приравнивание к нулю полученных производных дает систему алгебраических уравнений:

                                                

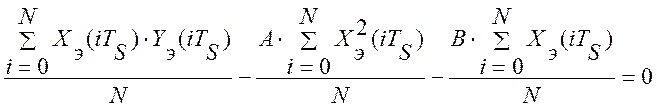
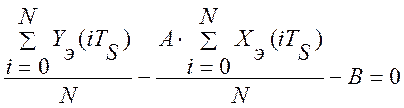
Если использовать в этой системе центрированные значения экспериментальных данных: , а , то все оценки нечетных начальных моментов в системе уравнений преобразуются в нечетные центральные моменты и становятся равными нулю. Поэтому система уравнений принимает после несложных преобразований следующий вид:

,                                            

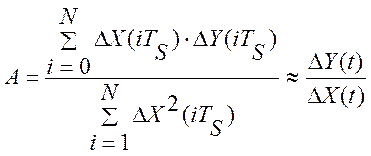где  ,  – текущие центрированные значения управляющего воздействия и критерия управления, измеренные с помощью технических средств автоматизации.

Коэффициент А есть не что иное как величина производной в рабочей точке при условии, что . Кроме того, в условиях нормального функционирования  есть не что иное как флуктуация управляющего воздействия, , вокруг своего математического ожидания.

Поэтому полученное выражение представляет собой алгоритм вычисления величины производной (в одномерном случае) или составляющих градиента (в многомерном случае) по данным нормального функционирования и, следовательно, алгоритм управления может быть сформулирован следующим образом (см. рис. 7.2):

– накапливаются экспериментальные данные по входу  и по выходу , по которым оцениваются величины математических ожиданий по входу  и по выходу  (блоки 2, 3) и производится центрирование (блоки 4, 5);

– с использованием полученного выражения вычисляются величины составляющих градиента по всем направлениям (блоки 6, 7, 9);

– делается шаг по переменным управления в сторону достижения экстремума (блоки 8, 10, 11).

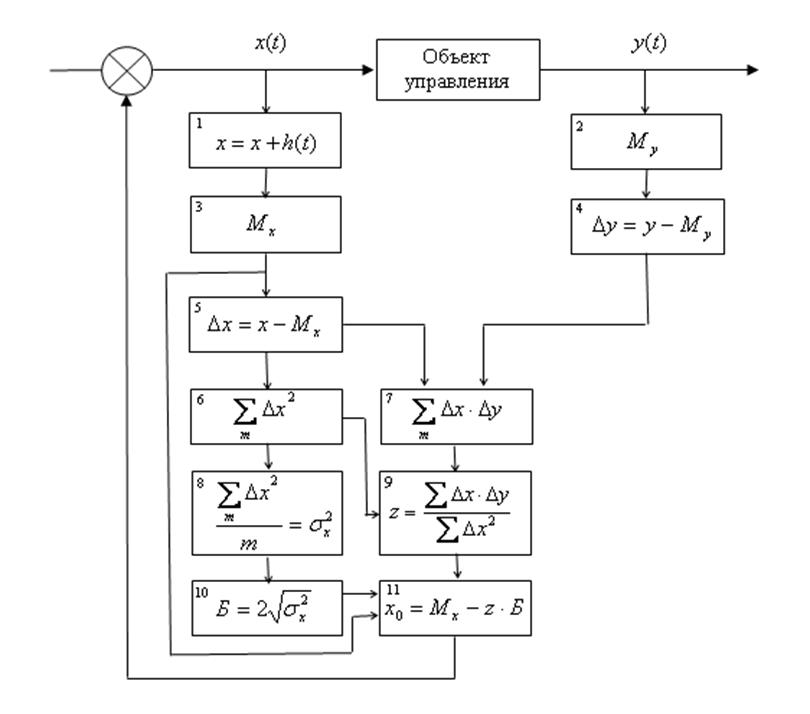
Рис. 7.2.  Блок-схема безмодельного алгоритма управления

Движение в сторону достижения экстремума осуществляется по алгоритму:

                         ,                                        

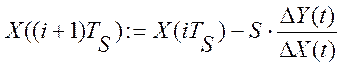где  ,  – текущее и предыдущее значения управляющего воздействия;  - настроечный коэффициент (обычно 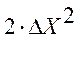);  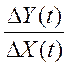- количественная оценка величины и знака производной в рабочей точке.

Алгоритм позволяет отслеживать дрейф критерия управления и следить за его перемещениями в реальном масштабе времени. Однако данный алгоритм не позволяет точно попасть в оптимум, а только следит за его перемещением.

Основным настроечным коэффициентом алгоритма является объем информации (), накапливаемой для идентификации знака и  величины производной в рабочей точке на критерии управления (см. рис. 7.3).

 

Рис. 7.3. К понятию настроечных коэффициентов программного обеспечения

Точность вычислений по рассматриваемому алгоритму возрастает при увеличении объема накопления, и поэтому предпочтительно большое количество измерений. Однако, чем больше измерений, тем дольше происходит накопление информации, тем дальше оптимальный режим «уплывает» и тем больше возрастают потери при управлении. Поэтому существует компромисс между увеличением объема выборки и скоростью дрейфа. Разрешение данного компромисса – это оптимальный режим функционирования алгоритма управления.

Применение этого алгоритма особенно выгодно в условиях больших (по амплитуде) изменений входных параметров для малоинерционных и безынерционных объектов, характеристики которых подвержены медленному дрейфу. Основными особенностями алгоритма  управления являются: