Система. Еквівалентні математичні моделі. Рівняння регресії. Специфікація входів і виходів системи

Система -1) сукупність  процесів, які взаємодіють між собою у часі; 2) сукупність множин і відображень S={T,V,X,Y,,f}

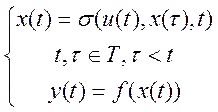
  1) проблема ідентифікації систем – побудова математичної моделі

2) виявлення або оцінювання поточних станів, зокрема, для розв’язання проблем прогнозування еволюції систем (спостережуваність)

3) формування входів, що забезпечують необхідне поводження систем (керованість)

           4) Проблема стійкості – проблема життєдіяльності системи

Математичні моделі наз. еквівалентними якщо при однакових входах вони дають однакові виходи

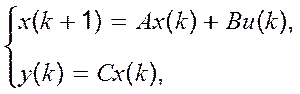
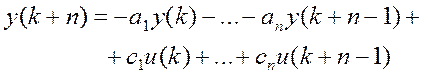
Передатною матрицею  лінійної системи, де  - комплексна змінна, називається перетворення Лапласа імпульсної перехідної матриці, тобто

.

Нехай на стаціонарну систему, що в початковий момент часу  перебуває в стані спокою, подається вхід  та  - його перетворення Лапласа. Перетворення Лапласа виходу , що відповідає цьому входу:

.

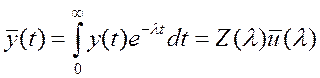            Таким чином , передатна матриця лінійної системи може розглядатися як модель зв’язку між її входами і виходами. Вона дозволяє передбачати реакцію системи, що перебуває в стані спокою. Якщо ж система не перебуває в стані спокою, то необхідно, щоб вона була повністю спостережуваною.

Для аналізу і при синтезі системи зручно зобразити у вигляді взаємозалежної сукупності окремих елементів – динамічних ланок.

Розглянемо лінійну дискретну стаціонарну модель системи

x(k +1) = Ax(k) + Bu(k),                     (5.21)

y(k) = Cx(k)                                  (5.22)

і з'ясуємо, як залежить образ дискретного перетворення Лапласа виходу y[0,∞] від образу Лапласа входу u[0, ∞].

Нехай x(k;x⁰,u[0,∞]) - процес, обумовлений рівнянням (5.21) і відповідний входу u[0, ∞] та початковому стану x⁰. Нехай x(λ) - образ Лапласа цього процесу. Застосувавши перетворення Лапласа до обох частин рівності (5.21), (5.22) і з огляду на властивості цього перетворення, одержуємо

λx^L(λ) – λx⁰= Ax^L(λ) + Bu(k),                   (5.23)

y(k)= Cx(k).                                  (5.24)

З (5.23) випливає х(λ) = (λI - A)^-1Bu(λ) + (λI- A)x⁰ і

y^l(λ) = C(λI - A)^-1Bu(λ) + λC(λ I - A)^-1x⁰   (5.25)

Для х⁰ = 0 одержуємо

y^L(λ) = W(λ)u(λ),                       (5.26)

де W(λ) = C(λI - А)^-1В.

Матриця W(λ) у (5.26) називається передатною матрицею системи (5.21), (5.22).

Згідно з (1.9) передатна матриця може бути обчислена як

.

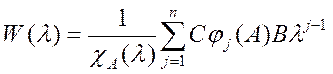Отже, елементами матриці W(λ) є раціональні функції від λ, причому степінь полінома в чисельнику кожної з них менше степеня полінома в знаменнику.

Поряд із системою (5.21), (5.22) розглянемо систему              z(k+1)=,                   (5.27)

y(k)=z(k).                                    (5.28)

Системи (5.21), (5.22) і (5.27), (5.28) називаються еквівалентними, якщо існує така невироджена матриця R, що заміна змінних стану за формулою x=Rz приводить систему (5.21),(5.22) до вигляду (5.27),(5.28).

Знайдемо, як виражаються матриці еквівалентної системи через матриці A, B, С. Маємо

Rz(k+1)=ARz(k)+Bu(k),

y(k)=CRz(k).                                (5.29)

З (5.29) одержуємо z(k+1)=R^-1ARz(k)+R^-1Bu(k). Отже,  = R^-1AR, = R^-1B і = CR.

Передатні матриці еквівалентних систем рівні. Дійсно,  (λ) = (λI -)^-1 = CR(λ I - R^-1AR)^-1R^-1B =

       =C(R(λ I - R^-1AR)R^-1)^-1B = C(λ I - A)^-1B = W(λ).

Матриці A, В і С характеризують, з одного боку, структуру лінійної системи, а з іншого - зв'язок між входом, станом і виходом. Керованість і спостережуваність також відбивають характер зв'язків стан-вхід і стан-вихід. Тому побудова матриць A, В, С і властивості керованості і спостережуваності взаємозалежні. З'ясуємо цю залежність.

Підпростір LХ називається інваріантним підпростором системи (5.21) щодо керувань u(k), якщо при будь-яких u(k) розв’язок x(k), що відповідає початковій умові x(0) = х⁰  L, при всіх k належить L.

Позначимо матрицю N_u=(В, AВ, . . . , А^п-1В). Нехай rgN_u=s і E_s - підпростір, натягнутий на стовпці матриці N_u. Тоді для будь-якого стовпця b_r матриці B вектор A^lb_r для l≥s лінійно виражається через вектори b_r, Ab_r, . . .,A^s-1 b_r.

Лема. Підпростір E_s є інваріантним щодо керувань u(k).

Ф. Під динамічною ланкою розуміють у загальному випадку абстрактний пристрій, що має вхід і вихід, і для якого задане рівняння, що пов'язує сигнали на вході і виході. Рівняння лінійної динамічної ланки має такий загальний вигляд:

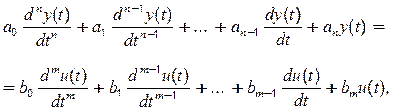 (5.21)

де - постійні коефіцієнти, .

Використовувати такий опис динамічної ланки в задачах аналізу і синтезу систем і об'єктів керування не раціонально, тому існують й інші форми опису і зображення динамічних ланок і систем у цілому. 

Піддамо рівняння (5.21) перетворенню Лапласа, вважаючи початкові умови нульовими і заміняючи оригінали сигналів їх зображеннями за Лапласом:

.

Використовуючи теореми лінійності і диференціювання для перетворення Лапласа, одержимо операторне рівняння, що пов'язує зображення вхідного і вихідного сигналів: