Система. Еквівалентні математичні моделі. Рівняння регресії. Специфікація входів і виходів системи, страница 3

Як приклад розглянемо так звану модель Кобба-Дугласа. Американські вчені Кобб і Дуглас поставили задачу отримати рівняння регресії, яке описує зростання обсягу продукції, виробленої в США протягом року, залежно від змін основного капіталу (виробничих потужностей) і витрат праці. За експериментальні дані  вони взяли статистичні дані за 1899-1922 роки, тобто у цьому випадку .

Нехай  означає обсяг випущеної продукції,  – обсяг основного капіталу та  – витрати праці у - му році.  Базовими функціями були обрані

  де .

Оскільки

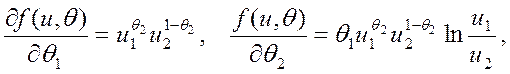
система (4.4) для цієї задачі має вигляд

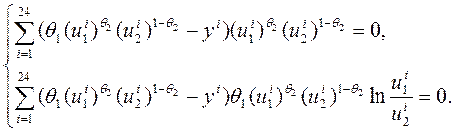
Це нелінійна система відносно двох невідомих  та . Розв’язання нелінійних систем рівнянь звичайно викликає великі труднощі. Тому виникає задача вибору таких базових функцій, щоб відповідна задача мінімізації  не була досить складною.

Існує ряд прийомів, які дозволяють зводити нелінійну систему вигляду (4.4) до лінійної. Одним з них є розв’язання задачі у логарифмічному масштабі даних. Наприклад, у задачі, що розглядається, після логарифмування обох частин рівняння регресії отримаємо

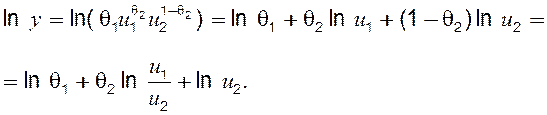
Позначимо:  та 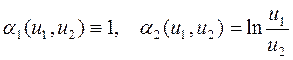. Тоді лінеаризована функція матиме вигляд

.                    (4.5)

Дані  та  перераховуються з  та  для

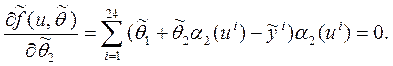Зміниться система (4.4):

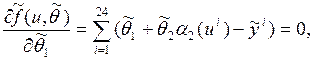
Це вже система двох лінійних рівнянь з двома невідомими  та , розв’язок  якої легко отримати. Остаточно маємо  та

Перш за все при побудові регресійної залежності необхідно визначитися з виглядом функції регресії. Якогось загального критерію на цей випадок не існує. Можна говорити про інтуїтивний підхід, що базується на дослідженні вхід-вихідних даних, які надані для побудови моделі.

На випадок, коли ці дані мають монотонний характер, вибір вигляду регресійної залежності можна здійснити за таблицею. Для цього за вхід-вихіднихми даними обчислюють середні значення u_ср та у_ср :

,  ,  ,

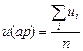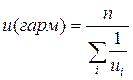Величина обчислюється так:

1) якщо  збігається з одним із вхідних , то ;

2) якщо  знаходиться між  і ,  знаходимо як ординату відповідної точки на відрізку прямої, що з'єднує вузли  і , за формулою

.

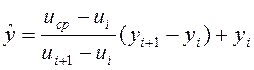Вибір базової функції для рівняння регресії здійснюється шляхом пошуку мінімального значення виразу 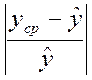 і відповідної йому функції.

Розглянемо при k=1,…,K скалярний процес y(k), який залежить від скалярного процесу u(k), і поставимо задачу виявити закон перетворення u(k) в y(k) на основі даних вхід-вихідного експерименту:

{()}.

Будемо шукати лінійну математичну модель, яка у середньоквадратичному змісті найкращим способом відтворює отримані  дослідні дані. Зафіксуємо n і будемо шукати  вхід-вихід  модель вигляду

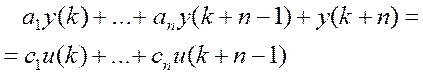            (4.19)

Це означає, що необхідно знайти коефіцієнти a₁,…a_n, c₁,…c_n рівняння(4.19).

Якщо y_M(k)-вихід, який обчислюється за моделлю і відповідає входу ū(k), то величину 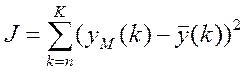 будемо розглядати як міру відхилення дійсного закону поведінки процесу від математичної моделі.  Такий її вигляд пояснюється тим, що обрана модель може передбачити реакцію системи для .

Як побачимо далі, обраний порядок моделі n має задовольняти умову K≥3n, що  забезпечить існування розв’язку задачі.

Перепишемо (4.19) у вигляді

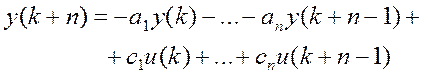       (4.20)

і введемо позначення:

 =col (₁ ,…, _n, _n+1,… _2n)=col(-a₁,…,-a_n, c₁,… c_n),

,

yⁱ=(i+n) для  i=1,…,N, де N=K-n.

Модель буде прогнозувати реакцію системи в і-му досліді за формулою

, і=1,...,N.              (4.21)

Для кожного і значення вектор-функції  відомі. Тому задача зводиться до знаходження такого значення векторного параметра , яке мінімізує середньоквадратичну похибку:

.

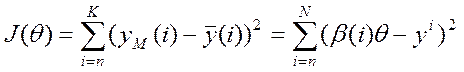           Маємо набір входів та виходів {(,_i),i=}={(),_i).

Для i-го експерименту одержимо похибку E_i()=u_i,q)-_i. У попередньому параграфі показано, що необхідна умова екстремуму  зводиться до розв’язання системи лінійних алгебраїчних рівнянь (4.7), тобто  відносно координат невідомого вектора .

У даному випадку матриця R має вигляд

 

           ...                   …