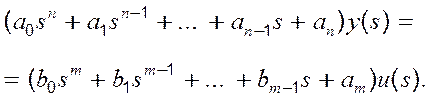Система. Еквівалентні математичні моделі. Рівняння регресії. Специфікація входів і виходів системи, страница 2

        (5.22)

Одержимо з (5.22) відношення зображень вихідного і вхідного сигналів:

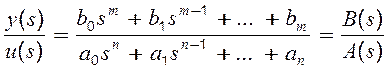.   (5.23)

Співвідношення (5.23) не залежить від зображень сигналів, визначається тільки параметрами самої динамічної ланки , має вигляд дробово-раціональної функції.

Відношення зображень вихідного і вхідного сигналів називають передатною функцією динамічної ланки                           .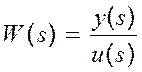

Рівняння  називають характеристичним рівнянням динамічної ланки, тому що знаменник передатної функції – це характеристичний поліном диференціального рівняння, яке описує динамічну ланку.

Частина процесу , що відповідає часу , називається перехідною, а інша, для якої  при , – усталеною. Так само можна говорити про усталену і перехідну частини процесу . Ця властивість системи визначається як стійкість. Тобто функціонування життєздатних систем передбачає наявність перехідного і усталеного режимів .

Розглядаючи систему в дискретні моменти часу, де , k = 0, ±1, ±2,..., як процес, який є предметом аналізу або прогнозу, можна так аналітично описати функціонування стійкої системи. Нехай задане мале число і нехай  – таке число, що  для . Назвемо перехідною ту частину процесу , яка відповідає , та усталеною ту, що відповідає . Для усталеної частини процесу вважаємо, що.

Якщо усталене значення  залежить лише від значення вхідного фактора , то існує така функція, що

                                     (4.1)

Рівняння (4.1) має назву рівняння регресії.

Реальну неперервну функцію , що описує залежність виходу системи від її входу, як правило, неможливо описати яким-небудь аналітичним виразом. Тому обирається деяка множина  функцій відомого вигляду та серед них шукається та, що найкраще описує функцію . Для цього на практиці звертаються до вхід-вихідного експерименту: подають на систему визначений набір тестуючих впливів  та реєструють значення , які використовуються для пошуку зазначеної вище функції.

Щоб виділити з множини  функцію, яка буде розглядатися як найкраща модель системи, тобто яка найкращим чином описує істинну модель , необхідно ввести деякий спосіб оцінки відхилень функцій з  від функції . Побудова в такий спосіб у формі деякого функціонала звичайно є евристичною процедурою. При розв’язуванні прикладних задач широко використовується квадратичний функціонал, мінімізація якого є основою методу найменших квадратів.

Отже, залежність встановленого скалярного виходу  від постійного входу  визначається рівнянням (4.1) з невідомою функцією  на основі результатів вхід-вихід експериментів . Вводиться множина  відомих функцій , де  – вектор параметрів цієї множини, і підбирається та з них, яка за експериментальними даними найближча до функції . Нехай ця функція відповідає набору параметрів . Тоді як модель розглядається рівняння  . Функції з  будемо називати базовими. Тут враховано, що аналітичний вираз функції  відомий.

При фіксованому значенні параметра , тобто фіксованій функції з , можемо для кожного  за експериментальними даними вирахувати значення  та відповідну цій функції похибку  опису істинної залежності. А саме:

  .

Задача полягає у виборі такого значення вектора , тобто такої функції з , що похибки  для всіх і будуть якнайменшими. Це досягається мінімізацією за  функціонала

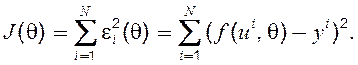             (4.2)

Функції  звичайно обираються диференційованими за  та такими, що мінімум  досягається для скінченних значень . Тоді за необхідною умовою екстремуму невідоме значення  є розв’язком рівняння , тобто задовольняє систему рівнянь

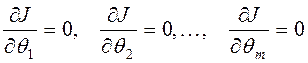.           (4.3)

У результаті для знаходження  отримаємо систему з  рівнянь з  невідомими:

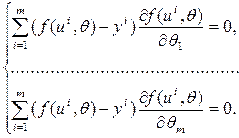               (4.4)

Після знаходження тих , що задовольняють систему рівнянь (4.4), необхідно кожне з них протестувати на мінімум.

Рівняння , яке приблизно описує причинно-наслідковий зв’язок між подіями  та , також має назву рівняння регресії.