Лабораторна робота №4
Сидоренко Олега
ПМ-71
Варіант №11
Дискретнy модель з простором станів дослідити на керованість та спостережуваність.
Модель з простором станів:
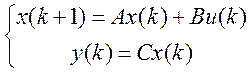
де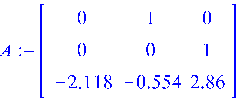 
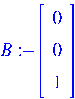
Вважаючи початковим стан системи
,
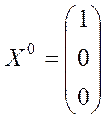розрахувати перехідні частини
процесів 
та 
та
побудувати їх графіки при заданих значеннях скалярного входу:
1) 
,
де 
.
2) 
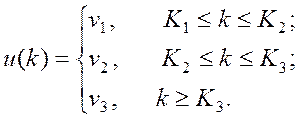
Тут К1=0; К2=Nв+2
К3=40;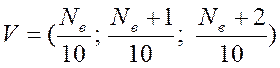 
, де 
- номер варіанта.
Розглянемо дискретну лінійну нестаціонарну модель системи:
x(k +1) = A(k)x(k) + B(k)u(k) + ƒ(k), (1)
y(k) = c(k)x(k)+G(k). (2)
Розглянемо двоточкову граничну задачу керування. Задано стани x0, x1 і моменти часу k0 і k1. Потрібно знайти таке керування на інтервалі часу [k0, k1], що переводить подію (k0, x0) у подію (k1, x1) по траєкторії системи (1).
Користуючись формулою загального розв’язку різницевого рівняння , випишемо умову x(k1) = x1, а саме:
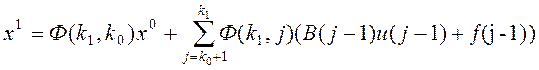. (3)
Отже, керування u(k), що розв’язує двоточкову граничну задачу, повинно забезпечити виконання рівності
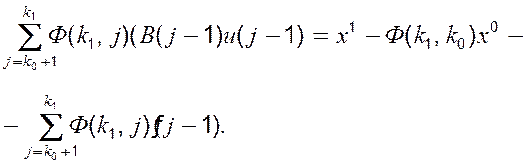(4)
Система (1) називається повністю k0-керованою, якщо для будь-якого x0 існують k1=k1(x0)<∞ і керування u[k0, k1] ,що переводить цю систему зі стану х0 у стан x=0.
Для знаходження умов повної керованості позначимо матрицю
(Ф(k1,k0 + 1)B(k0),Ф(k1,k0+2)B(k0+1),…,Ф(k1,k1)B(k1– 1))
у лівій частині системи рівнянь (4) як V(k0, k1), стовпець у правій частині (4) через v(k0, k1) і запишемо це рівняння у вигляді
V(k0, k1)U = v(k0, k1), (5)
де U — col(u(k0),u(k0 + 1),…,u(k1-1)).
За теоремою Кронекера-Капеллі рівняння (5) має розв'язок відносно U, якщо rg(V(k0,k1),v(k0,k1))=rgV(k0,k1). Якщо detФ(k0,k1) ≠ 0, то v(k0,k1) може бути будь-яким вектором з R, тому достатньою умовою повної k0-керованості є
rgV(k0,k1) = п. (6)
Матриця V(k0, k1) має розмірність n´(k1- k0)m,тому умовою на k0 для повної керованості є (k1-k0)≥n.
Розглянемо тепер випадок стаціонарних систем. У цьому випадку Ф(k1, j) = Ak1-j, тому критерій (6) набуває вигляду
rg(B, АВ,..., Аn-1B) = n. (7)
Умова (7) називається критерієм Калмана.
Розглянемо модель (1), (2) лінійної системи, і нехай на інтервалі [k0, k1] вимірюються вхід u[k0, k1] і вихід y[k0, k1] цієї системи. У моменти k0 і k1 ця система перебуває в деяких станах x0 і x1.
Задача виявлення (оцінювання) стану х0 на основі даних u[k0, k1] і y[k0, k1] називається задачею спостереження, а виявлення стану x1 - задачею діагностики.
Згідно з (1) і (2) кожен стан х*, поклавши G(k) = 0 s користуючись фундаментальною системою розв’язків (1), задовольняє систему рівнянь
C(k0)x* = y(k0),
C(k0+1)Ф(k0+1, k0)x* = y(k0+1),
……………………………………… (8)
C(k0+k1)Ф(k0+k1, k0)x* = y(k0+k1).
Множина тих x, що задовольняють систему рівнянь (8), являє собою площину відповідної розмірності в Rn. Введемо позначення:
,
.
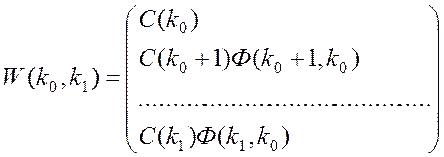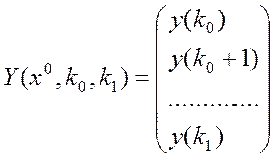Тоді (8) перепишеться у вигляді
W(k0, k1)x* = Y(x0, k0, k1). (9)
Система (1), (2) називається повністю k0 спостережуваною на [k0,k1], якщо між її станами x(k0) і виходами y[k0,k1] існує взаємно-однозначна відповідність.
Очевидно, система (1), (2) цілком k0-спостережувана тоді і тільки тоді, коли рівняння W(k0,k1)x=0 має єдиний розв’язок . Останнє ж еквівалентно умові
rgW(k0, k1) = n. (10)
Таким чином, повна k0-спостережність визначається властивостями (k1–k0+1)´n-матриці W(k0,k1).
Збільшення інтервалу спостереження призводить до зростання розмірності матриці W(k0, k1). Застосувавши критерій Грама, можна звести задачу до знаходження рангу матриці розміру п´п. Для цього розглянемо n´n-матрицю R(k0, k1) =W*(k0, k1) W(k0, k1) або в докладному записі
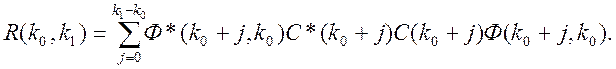
Оскільки rgR(k0,k1)=rgW(k0,k1), то критерієм повного k1-спостереження на [k0, k1] є умова
rgR(k0, k1) = п. (11)
Розглянемо тепер випадок стаціонарних систем, тобто коли матриці A(k), B(k) і C(k) не залежать від k0. У цьому випадку Ф(k0+ k, k0)=Ak і умова (5.15) не залежать від k. Критерій повної спостережуваності (5.15) у цьому випадку має такий вигляд:
rg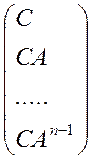
= n, (12)
Виконати дане завдання можна використовуючи різні пакетні програми. Наприклад, досить легко виконати його, використовуючи бібліотеку лінійної алгебри пакету Maple.
> with(linalg):
> y(k+3):=-2.118*y(k)-0.554*y(k+1)+2.86*y(k+2)-0.000042*u(k)+0.000075*u(k+1)+0.0000047*u(k+2);
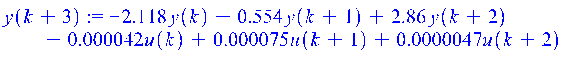
> A:=matrix(3,3,[0, 1, 0, 0, 0, 1, -2.118, -.554, +2.86]);
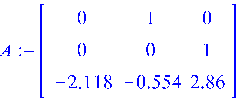
> B:=matrix(3, 1, [0, 0, 1]);
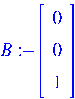
> C:=matrix(1,3,[-0.000042,0.000075,0.0000047]);
> 
> 
> 
> 
> 
> 
> 
> 
> 
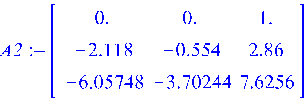
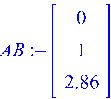
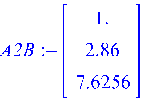
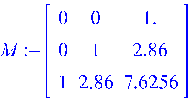
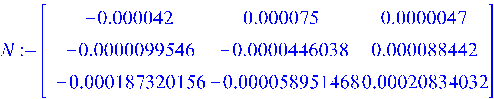
Визначення режимів функціонування системи:
> restart:
> with(LinearAlgebra):
with(plots):
A:=<<0| 1| 0>, <0| 0| 1>, <-2.118|-0.554|2.86>>:
B:=<0, 0, 1>:
C:=<-0.000042|0.000075|0.0000047>:
P:=<0.0015| -0.01| 0.005>:
x:=<1, 0, 0>:
N:=100:
x1:=array(0..N):
x2:=array(0..N):
x3:=array(0..N):
y:=array(0..N):
II:=array(0..N):
for i from 0 by 1 to N do
x1[i]:=Vector(x)[1]:
x2[i]:=Vector(x)[2]:
x3[i]:=Vector(x)[3]:
M:=Multiply(A,x):
U:=DotProduct(P,x):
L:=ScalarMultiply(B,U):
x:=Add(M,L):
y1:=Multiply(C,x):
y[i]:=y1:
II[i]:=i:
end do:
a:=convert(II,'list'):
b:=convert(y,'list'):
plot(a,b,style=Point);
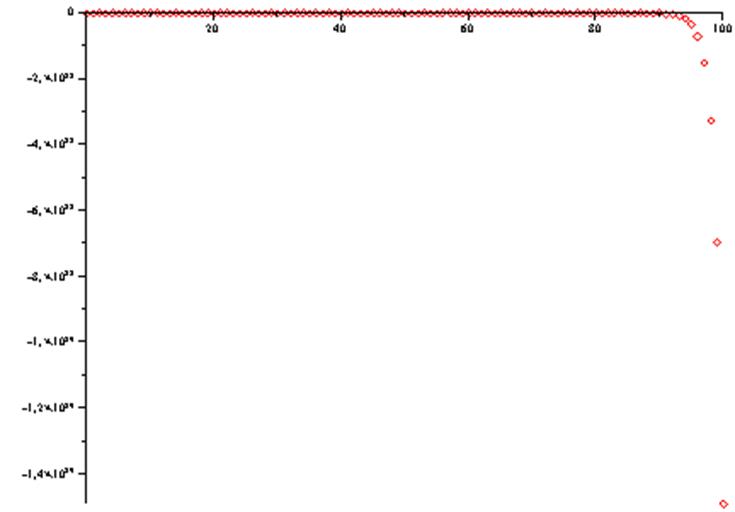
> restart;
with(LinearAlgebra):
with(plots):
A:=<<0| 1| 0>, <0| 0| 1>, <-2.118|-0.554|2.86>>:
B:=<0, 0, 1>:
C:=<-0.000042|0.000075|0.0000047>:
P:=<0.0015| -0.01| 0.005>:
x:=<1, 0, 0>:
N:=100:
x1:=array(0..N):
x2:=array(0..N):
x3:=array(0..N):
y:=array(0..N):
II:=array(0..N):
UU:=array(0..N):
for i from 0 by 1 to N do
if (i<=14.5) then U:=1.1
elif (i>14.5) and (i<=40) then U:=1.2
else U:=1.3
end if:
x1[i]:=Vector(x)[1]:
x2[i]:=Vector(x)[2]:
x3[i]:=Vector(x)[3]:
M:=Multiply(A,x):
L:=ScalarMultiply(B,U):
x:=Add(M,L):
y1:=Multiply(C,x):
y[i]:=y1:
II[i]:=i:
UU[i]:=U:
end do:
a1:=convert(II,'list'):
b1:=convert(y,'list'):
plot(a1,b1,style=Point);
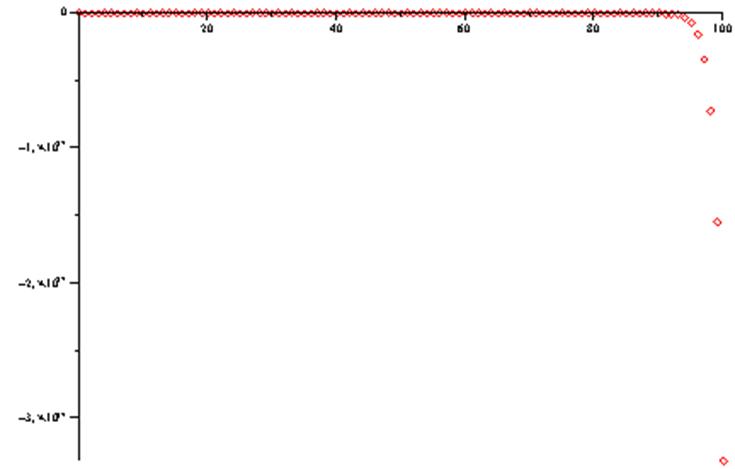
У даній лабораторній роботі було досліджено дискретну стаціонарну лінійну детерміновану модель з простором станів, що має вигляд:
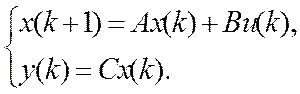
В результаті було визначено, що дана модель є керованою та спостережуваною. Було побудовано графіки режимів функціонування системи ( усталеного та перехідного періодів), за якими можна зробити висновок, що дана система не є стійкою.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
