Елементи алгебри матриць (Лабораторна робота № 1)

Сумський державний  університет

Кафедра інформатики

Лабораторна робота№1

на тему:

“ Елементи алгебри матриць”

з дисципліни:

“Теорія систем та математичне моделювання”

Виконала

студентка групи ін-61/2

Берко Анна

Суми 2008

Завдання 1.1

Для матриці А визначється:

1)  характеристичний поліном та спектр матриці ;

2)  матрицю переходу до матриці Фробеніуса;

3)  подібні матриці Фробеніуса та Жордана.

	-0,83	0,31	-0,18	0,22	1,71
7	-0,21	-1,00	0,33	0,22	-0,62
	0,32	-0,18	-0,95	-0,19	0,89
	0,12	0,28	-0,14	-1,00	-0,94

Рангом матриці називається найвищий з порядків її мінорів, відмінних від нуля. Позначення rgA. Відмінний від нуля мінор матриці A , порядок якого r= rgA , називається базисним мінором.

Основними методами обчислення рангу є метод обвідних мінорів та метод елементарних перетворень.

1) Характеристичний поліном –це детермінант матриці (А-λЕ):

 В основу математичної класифікації систем покладено визначення системи множин і відображень. Стосовно структури множини Т системи розбиваються на два класи. Якщо Т збігається з множиною дійсних чисел R, то рівняння ( 3.1) і (3.2) визначають клас неперервних за часом систем. Якщо ж Т = {t_k : k = 0, ±1, ±2,..., і t_k-1 < t_k}, то система належить класові дискретних за часом систем. Останні найбільш широко використовуються в математичній економіці.

Якщо у випадку дискретних за часом систем визначити відображення σ як f(t_k,x,u) = σ(t_k+1;t_k,x,u), то відображення σ є загальним розв’язком різницевого рівняння

x(t_k+1) = f(t_k, x(t_k), u(t_k)),

що випливає з аксіом, які задовольняє σ . У такому випадку математичною формою представлення системи можуть бути рівняння (3.1) і (3.3). Оскільки ,: k = 0, ±1, ±2,...,  то в загальному випадку дискретна математична модель має вигляд

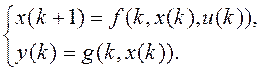                      (3.3)

Системи можна розбити ще на два класи - детерміновані і стохастичні. Модель детермінованих систем не містить випадкових величин. Якщо у рівняння (3.1), (3.2) або (3.3) входять величини, що мають ймовірнісний характер, то такі системи називають стохастичними.

Розглянемо детерміновані системи і проведемо їх класифікацію.

Система (3.3) називається кінцевим автоматом, якщо вона дискретна за часом і множини U, Y і X мають скінченне число елементів.

У теорії кінцевих автоматів множини U і Y називають вхідним і вихідним алфавітами.

Система (3.3) називається скінченновимірною, якщо X, Y і U є скінченновимірними лінійними просторами.

Далі будуть розглядатися тільки скінченновимірні системи.

Система (3.3) називається стаціонарною, якщо функції f і g не залежать від k. У цьому випадку дискретна модель системи задається рівняннями

x(k+1)= f(x(k), u(k))     ,                      (3.4)          y(k) = g(x(k)).                                  (3.5)

Система називається лінійною, якщо множини X, U, і Y є лінійними просторами, відображення f лінійне по х і и, відображення g лінійне по х.

У цьому випадку дискретна нестаціонарна стохастична лінійна математична модель має такий вигляд:

x^a (k+1)=A^a(k)x(k) + B^a(k)u^a(k)+ f^a(k),       (3.6)                    y^a(k) = C^a(k)x(k) + G^a(k),                   (3.7)

де f ^a(k),G^a(k) - відображення з Т в X і A^a(k), B^a(k) і C^a(k) -лінійні оператори.

Якщо в просторах X, U і Y вибрати базиси, то елементи x^а,u^а,y^а, f ^a і G^a будуть представлені n-вектором x , m-вектором и, l-вектором y, n-вектором f і l-вектором G, а оператори A^a (k), B^a(k) і C^a(k) – n´n-матрицею A(k), n´m-матрицею B(k) і l´n-матрицею C(k).

Тоді закон поведінки системи в матричному вигляді подається як

x(k + 1) = A(k)x(k) + B(k)u(k)+ f(k),

y(k) = C(k)x(k)+G(k),

де x(k)єRⁿ, y(k)єR^l і u(k)єR^m.

Лінійний кінцевий автомат також називають лінійною послідовною машиною.

Матриці А і В називаються подібними, якщо існує невироджена матриця R, така, що R^-1AR=B.

Розглянемо матрицю λI—А і обчислимо матрицю (λI — А)^-1, що часто використовується в додатках. Для цього скористаємося формулою

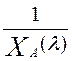
(λI-A)^-1= Q_iλ^i-1  ,         (1.4)

де Q₁,…,Q_n -n´n-матриці. Помноживши обидві частини рівності (1.4) на (λI-А),одержимо

X_A(λ)=(λI-A)Q_iλ^i-1.            (1.5)

Характеристичні поліноми подібних матриць збігаються. Дійсно,

)=det(lI-R^-1АR)=det(R^-1(λI-A)R)=

=detR^-1det(λI-A) detR=det( λI-A)=X_A(λ). З рівності (1.5) випливає Х_A(A)=0, тобто значенням характеристичного полінома матриці від самої матриці є нульова матриця. Цей факт називається теоремою Гамільтона – Келі

> with(LinearAlgebra):

> AA:=<<-0.83|0.31|-0.18|0.22>,<-0.21|-1.00|0.33|0.22>,<0.32|-0.18|-0.95|-0.19>,<0.12|0.28|-0.14|-1.00>>;

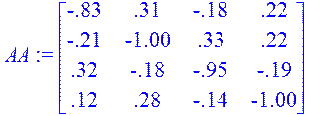
>  Xa:=CharacteristicPolynomial(AA,x);

2) Спектр матриці   

Спектр матриці – множина всіх коренів характеристичного полінома утворює спектр матриці.

 > Spekter := solve( {Xa} );

 

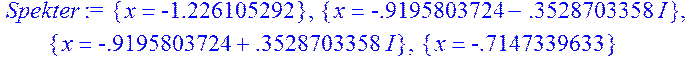
Множина усіх власних значень матриці А називається її спектром. Власні значення також називають модами матриці. Алгебраїчна проблема власних значень формулюється таким чином: знайти числа  та вектори , , для яких

,                                 (1.3)

де А – задана матриця з множини Mat_n(C) (n×n) – матриць з комплексними єлементами; С – множина комплексних чисел. Числа l називаються власними числами (значеннями), а відповідні вектори х – правими власними векторами матриці А.

Множина

утворює підпростір векторів простору Cⁿ, і цей підпростір має розмір

Число є тоді і лише тоді власним числом матриці А, коли L(l)¹0, тобто коли , і .Многочлен 

називається характеристичним многочленом матриці А, і його корені є власними значеннями А. Якщо l₁,...,l_k є різними коренями X_A(l), то .

Число s(l_і)=s_і називається кратністю власного значення, точніше алгебраїчною кратністю.Похідними поліномами матриці А будемо називати поліноми φ₁(λ),…, φ_n(λ), визначені як

φ_n(λ)=1,        φ_i-1(λ)=λφ_i(λ)+a_iλ⁰  для   i=n,n-1,...,2.        (1.7)