Лабораторна робота №5
Сидоренко Олега
ПМ-71
Варіант №11
Перевірити на асимптотичну стійкість системи, отримані в завданні 4,5
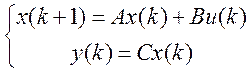
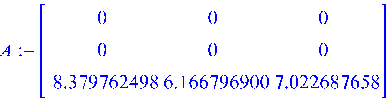
Для асимптотичної
стійкості системи необхідно і достатньо, щоб модулі всіх власних чисел матриці
А були менше одиниці.
Перевіримо чи виконуються умови теореми.
> with(LinearAlgebra):
> A:=Matrix([[0, 1, 0],[ 0, 0, 1],[8.38, 6.167, 7.022]]);
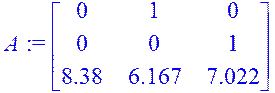
>
> Xa:=CharacteristicPolynomial(A,lambda);
![]()
> Specter:= solve ({Xa});
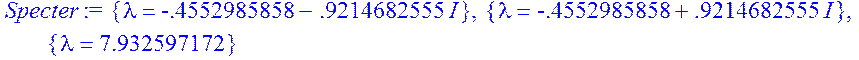
Умова теореми не виконується, так як одне з власних чисел більше одиниці, це означає, що система не є асимптотично стійкою.
Завдання 3,1:
Промоделювати на ЕОМ роботу двигуна постійного струму, яка описується рівнянням
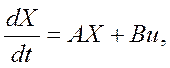
де
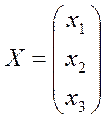 ,
, 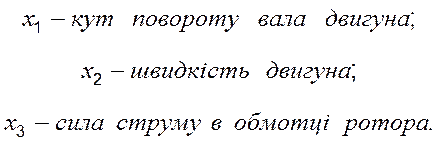
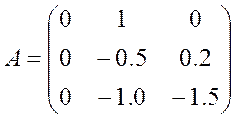 ,
,  ,
,
![]() .
.
Тут константа k=3; ![]() .
Початковий стан нашої системи визначається вектором
.
Початковий стан нашої системи визначається вектором 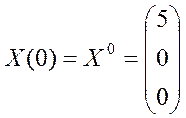 .
.
Часовий
інтервал визначення станів системи [0,20]. Результат треба видавати з кроком ![]() .
.
Розв’язання:
Спочатку розв’язуємо систему
диференціальних рівнянь в загальному випадку, а потім на інтервалі [0,20], з кроком ![]() .
.
> restart:
A:=Matrix(3,3):
A:=Matrix([[0,1,0],[0,-0.5,0.2],[0,-1,-1.5]]);
B:=Matrix(3,1):
B:=Matrix([[0],[0],[3]]);
P:=Matrix([[-1.1,-1.1,0]]);
X:=Matrix([[x1(t)],[x2(t)],[x3(t)]]);
D_:=Matrix(A.X+B.(P.X));
sys:=diff(x1(t),t)=D_[1,1],diff(x2(t),t)=D_[2,1],diff(x3(t),t)=D_[3,1];
fcns:={x1(t),x2(t),x3(t)}:
sys;
ds:=evalf(dsolve({sys,x1(0)=5,x2(0)=0,x3(0)=0},fcns));
for t from 0 by 0.8 to 20 do
evalf(ds);
end do:
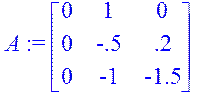
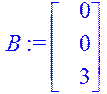
![]()
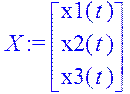
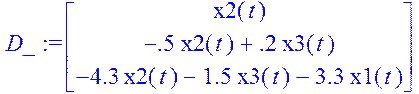
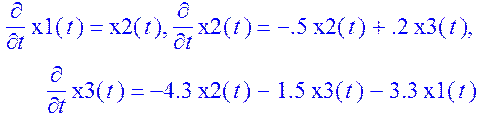
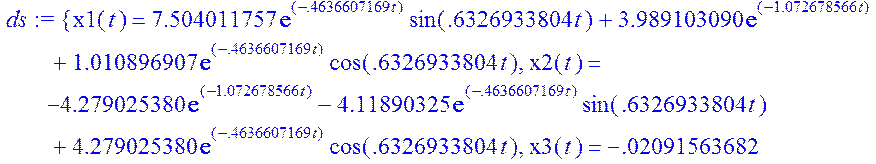
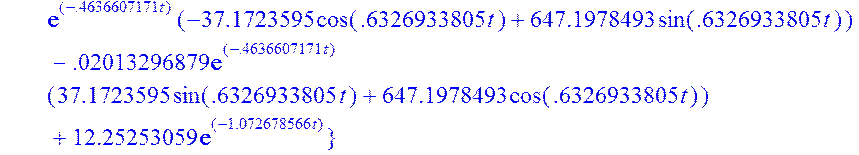
> xx3:=(-12.25253053*cos(.6326933805*tt)-14.28494512*sin(.6326933805*tt))*exp(-.4636607171*tt)+12.25253059*exp(-1.072678566*tt);
xx2:=-4.279025380*exp(-1.072678566*tt)-4.11890325*exp(-.4636607171*tt)*sin(.6326933804*tt)+4.279025380*exp(-.4636607171*tt)*cos(.6326933804*tt);
xx1:=7.504011757*exp(-.4636607171*tt)*sin(.6326933804*tt)+3.989103088*exp(-1.072678566*tt)+1.010896906*exp(-.4636607171*tt)*cos(.6326933804*tt);
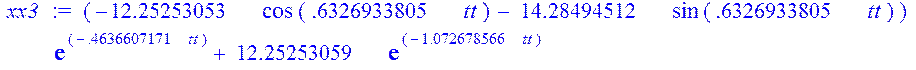
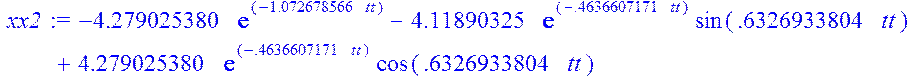
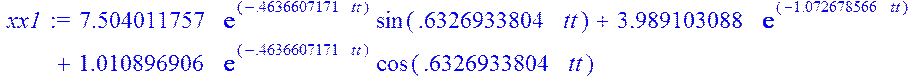
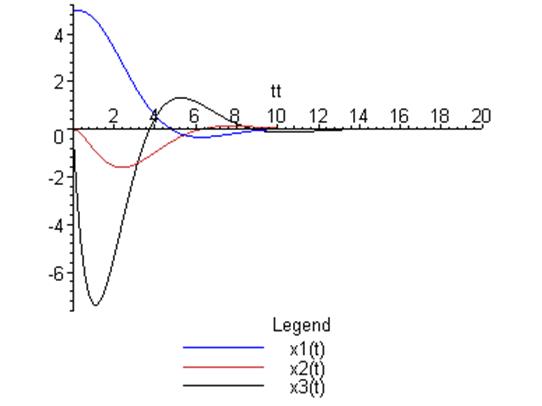
> plot([xx1,xx2,xx3],tt=0..20,color=[blue,orange,black],legend=["x1(t)","x2(t)","x3(t)"]);
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.