Татарченко Аліна ІН-91
Лабораторна робота №2
Завдання 4.4 Побудувати дискретну лінійну модель вхід – вихід за
показниками входів у систему ![]() та її реакцій
та її реакцій ![]() , що вимірювалися в однакові моменти часу
, що вимірювалися в однакові моменти часу ![]() разів (дані з табл. 4.4).
разів (дані з табл. 4.4).
Варіант 10:
|
10 |
U={3.2;2.8;1.6; 1.55;1.9;2.01;2.5;2.7;3.1;3.6;4.1} Y={6.3; 5.2; 3.1;2.9; 1.5;2.2; 3.8; 3.9; 4.1; 4.9;5.2} |
Хід роботи
Загальний вигляд моделі буде такий
![]()
Вибір вигляду моделі визначається з передбачення, що реакція системи в момент часу (k+n) залежить від входів виходів в якийсь попередній n моментів часу.
Невідомі коефіцієнти моделі будемо шукати за
методом найменших квадратів за умови, що модель найкращим чином буде
передбачати вихідні дані, які є відомими. За критерій оптимальності передбачень
будемо обирати 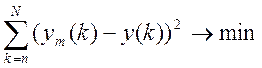
![]() - похибка
- похибка
Для того, щоб побудувати модель вхід-вихід потрібно:
n – порядок моделі – кількість моментів часу які є впливовими на реакцію системи в початковий момент.
Виберемо порядок моделі:
n визначається з: 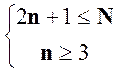 , N=10
, N=10
![]()
.Тоді вона набуде вигляду
![]() . Використовувати її можна для
. Використовувати її можна для ![]() , щоб спрогнозувати відповідні відомі
значення реакції системи. При
, щоб спрогнозувати відповідні відомі
значення реакції системи. При
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]()
Модель не може передбачити всіх експериментальних значень виходів, а може передбачити тільки з моменту часу n.
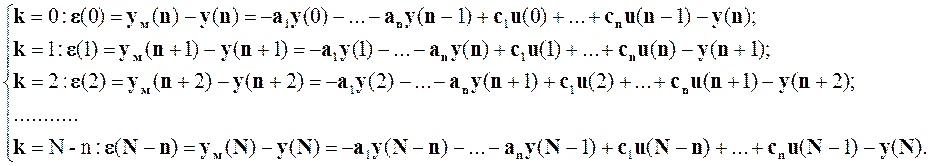
В матричному вигляді система буде виглядати так:
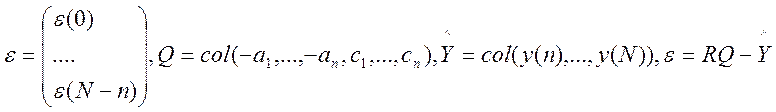 ,
,
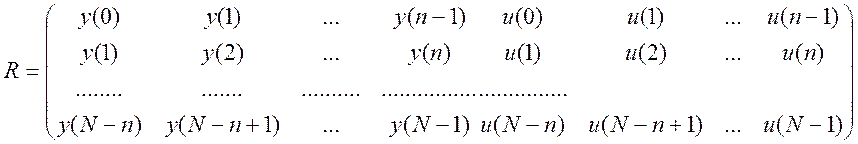 .
.
Метод найменших квадратів: 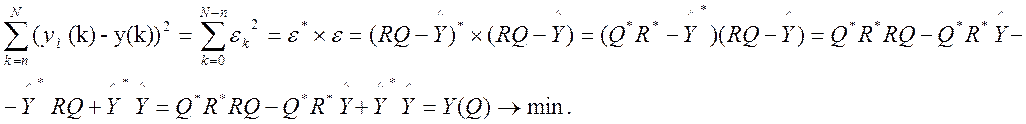
![]()
Достатня умова існування екстремуму в МНК виконується завжди – сума квадратів відхилень не буде мати максимуму, лише мінімум.
Необхідна умова існування екстремуму - 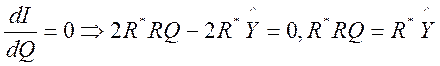 - СЛАР, яку необхідно розв’язати відносно Q.
- СЛАР, яку необхідно розв’язати відносно Q.
1.) За даними
значеннями входів ![]() і
виходів
і
виходів ![]() ,
побудувати матрицю R
,
побудувати матрицю R
![]()
![]() ...
... ![]()
![]() …
… ![]()
![]()
![]() ...
... ![]()
![]() ...
... ![]()
R= ………………………………..…………..….....
![]() ...
... ![]()
![]() …
…![]()
> R:=<<2.4|2.9|3.6|4.2|1|2|3|4>, <2.9|3.6|4.2|5.1|2|3|4|5>,<3.6|4.2|5.1|5.8|3|4|5|6>,<4.2|5.1|5.8|6.3|4|5|6|7>,<5.1|5.8|6.3|7.8|5|6|7|8>, <5.8|6.3|7.8|9.5|6|7|8|9>>;

2.)Визначити транспоновану матрицю R*
> R1:=transpose(R);

3.)Отримати матрицю А=R*∙R
> A:=multiply(R1,R);
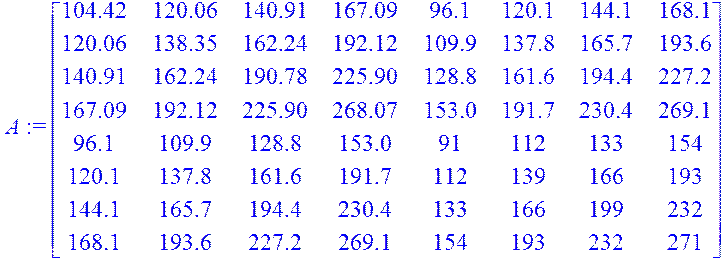
4.) Ввести ![]()
> Y1:=<4.2,5.1,5.8,6.3,7.8,9.5>;

5.) Отримати матрицю B = R*![]() .
.
> B:=multiply(R1,Y1);
![]()
6.) Розв'язати СЛАР Q=(R*R)-1![]() R*
R*![]() .
.
> A2:=inverse(A);

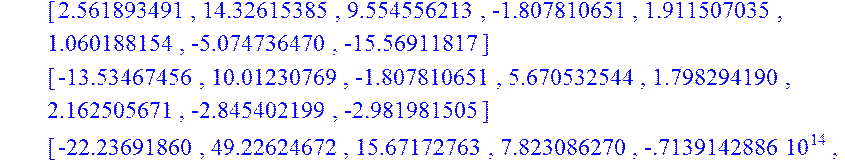

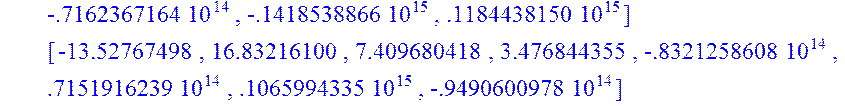
> Q:=multiply(A2,B);
![]()
Отже, модель детермінована модель вхід-вихід для даної задачі буде мати такий вигляд:
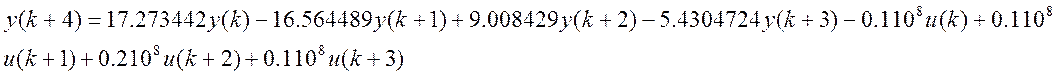
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.