Побудова дискретної лінійної моделі вхід-вихід за показниками входів у систему та її реакцій (Лабораторна робота № 2. Варіант 5)

Байрамова Ельчина

Група Ін-51

Лабораторна робота №2

Варіант 5

Завдання.

Побудувати дискретну лінійну модель вхід – вихід за показниками входів у систему  та її реакцій , що вимірювалися в однакові моменти часу  разів:

U={1.1; 1.8; 2.1; 3.6; 4.1; 4.8; 5.2; 5.9 ;6.1; 6.4}

Y={0.1; 0.8; 0.9; 1.7; 2.6; 3.4;4.3; 5.0; 5.8; 6.3;}

Практична реалізація

Математичне обгрунтування

Будемо шукати лінійну математичну модель, яка у середньоквадратичному змісті найкращим способом відтворює отримані  дослідні дані.

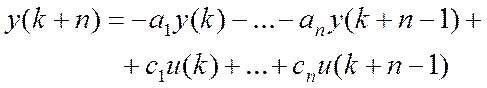
Будемо використовувати метод найменших квадратів для отримання динамічних дискретних моделей вхід-вихід.

За умовою K=11; k=1,2,…,K;

Виберемо порядок моделі n=3   (2n+1<=K).  Тоді вона набуде вигляду

Задача полягає у знаходженні коефіцієнтів  -а₁, -а₂, -а₃ та с₁, с₂, с₃.

Знайти їх можна, використовуючи метод найменших квадратів. Середньоквадратичною похибкою є 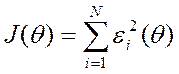. Її можна представити у вигляді

,

де  =col (₁ ,…, _n, _n+1,… _2n) = col(-a₁,…,-a_n, c₁,… c_n)

,

                …         …    .

                …     …    .

R=    ……………………………………..…………..………..

      ….  

Необхідна умова екстремуму J зводиться до розв’язку системи лінійних алгебраїчних рівнянь . Розв’язавши її відносно  ми і отримаємо невідомі коефіцієнти -а₁, -а₂, -а₃ та с₁, с₂, с₃

Розв’язання

Систему   розв’язуємо матричним способом за допомогою пакету Mathcad . 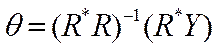, де - транспонована матриця R

 

 

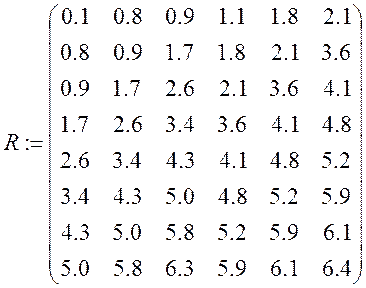
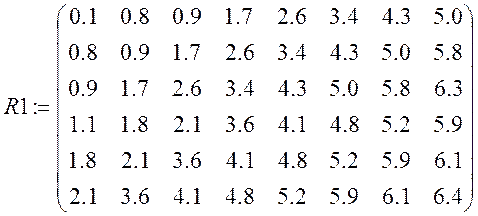
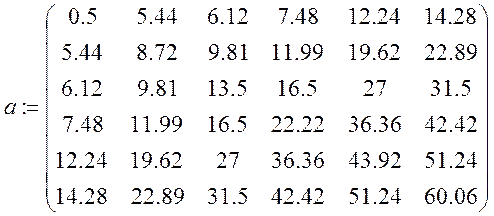
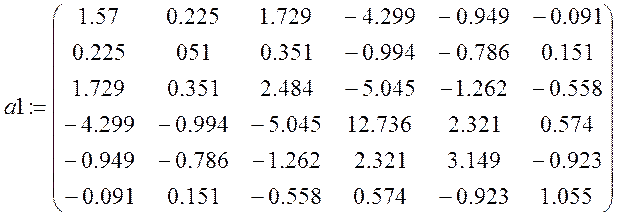
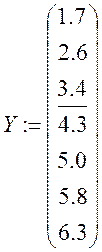
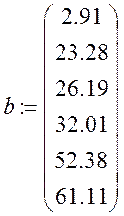
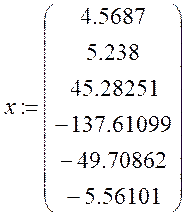
Отримана модель вхід-вихід має такий вигляд:

y(k+3) = 4.5687y(k)+5.238y(k+1) +45.28251y(k+2)-137.61099u(k)-49.70862u(k+1)-5.56101 u(k+2).