Лабораторна робота №8
ст.. гр.. ІН-51
Байрамова Ельчина
Завдання 7 Побудувати модальне
керування системою з відомою моделлю з простором станів, де матриця ![]() , за заданим спектром.
, за заданим спектром.
|
Варіант |
Заданий спектр |
Спектр матриці А |
|
15 |
|
|
За заданим спектром – коренями квадратного рівняння – відтворимо заданий характеристичний поліном.
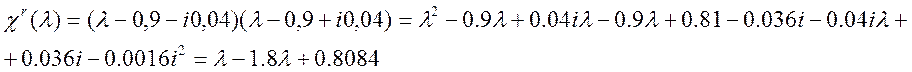
Його коефіцієнти ![]()
За спектром матриці А визначимо її характеристичній поліном:
![]()
Його коефіцієнти ![]()
Закон керування системою шукаємо у вигляді ![]() . При цьому невідому матрицю
. При цьому невідому матрицю ![]() знаходимо за формулою
знаходимо за формулою ![]() . Матриця R є матрицею ,що дозволяє
отримати еквівалентну заданій модель з простором станів, у якої подібною до матриці
А буде її матриця Фробеніуса. Отже,
. Матриця R є матрицею ,що дозволяє
отримати еквівалентну заданій модель з простором станів, у якої подібною до матриці
А буде її матриця Фробеніуса. Отже,
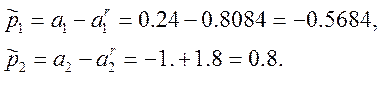
P = (-0.5684, 0.8)
Завдання 8. Побудувати естиматор, використовуючи дані з лабораторної роботи №7.
Реалізація завдання за допомогою пакету Maple:
> with(LinearAlgebra):
> a1:=0.24; a2:=-1; a1z:=0.8084; a2z:=-1.8;
![]()
![]()
![]()
![]()
> p1:=a1-a1z; p2:=a2-a2z;
![]()
![]()
> P:=Matrix([[p1],[p2]]);
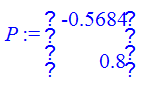
> FbA:=Matrix([[0,1],[-a1,-a2]]);
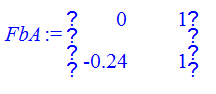
> fi2:=IdentityMatrix(2);
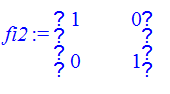
> temp:=ScalarMultiply(fi2,a2);
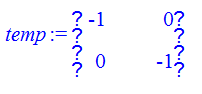
> fi1:=Add(FbA,temp);
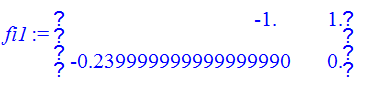
> C:=Matrix([1,0]);
![]()
> r1:=Multiply(C,fi1); r2:=Multiply(C,fi2);
![]()
![]()
> Rl:=<<r1>,<r2>>;
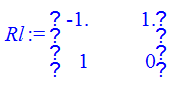
> Rl_obr:=MatrixInverse(Rl);
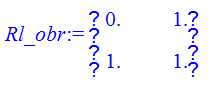
> L:=Multiply(Rl_obr,P);
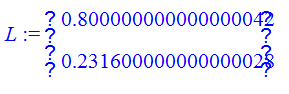
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.