Лабораторна робота № 7
Завдання:
Задана дискретна лінійна стаціонарна детермінована математична модель з простором станів
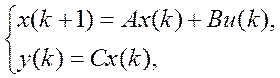
де ![]() , спектр матриці А та
матриця С задані в таблиці .Побудувати модальне керування системою за
заданим спектром з таблиці .
, спектр матриці А та
матриця С задані в таблиці .Побудувати модальне керування системою за
заданим спектром з таблиці .
|
Варіант |
Заданий спектр |
Спектр матр. А |
Матриц. С |
|
21 |
|
|
(4,1;0,2) |
Теоретичний матеріал:
Модальне керування ставить за мету досягнення
усталеного режиму функціонування системи, що характеризується асимптотичною
стійкістю системи.Оскільки задана модель є лінійною, то ![]() ,
,
![]() - матриця розмірністю
- матриця розмірністю ![]() .
.
![]() .
.
Так як асимптотична стійкість системи визначається
власними значеннями системи, то керування ![]() здійснюється
за заданим спектром.
здійснюється
за заданим спектром. ![]()
![]()
![]() .
.
Підставимо у перше рівняння: ![]() .
.
Врахування заданого спектру для досягнення асимптотичної стійкості системи означає, що існує як зразок інша система, подібна до досліджуваної, що має властивість асимптотичної стійкості.
Задача модального керування полягає в побудові такої матриці
![]() , щоб власні числа матриці
, щоб власні числа матриці ![]() збігалися з заданим спектром
збігалися з заданим спектром ![]() . Побудова матриці
. Побудова матриці ![]() здійснюється за умови , що задана модель і
наслідувана модель будуть еквівалентними.У еквівалентних моделей матриці
подібні, а отже характеристичний поліном і спектр однакові.
здійснюється за умови , що задана модель і
наслідувана модель будуть еквівалентними.У еквівалентних моделей матриці
подібні, а отже характеристичний поліном і спектр однакові.
![]() .
.
Розв’язання:
Характеристичний поліном матриці А другого порядку в загальному вигляді є таким:
![]() .
.
Знайдемо його за заданим спектром:
![]() .
.
Отже, коефіцієнти характеристичного полінома ![]() ,
, ![]() .
.
За заданим спектром – коренями квадратного рівняння – відтворимо заданий характеристичний поліном.
![]() .
.
![]() ,
, ![]() .
.
Оскільки
за умови ![]() , то
, то ![]() буде
мати вигляд:
буде
мати вигляд:
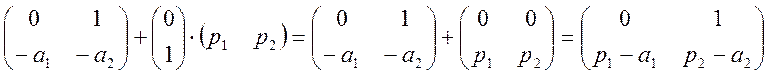
Отже матриця ![]() також записана у формі
Фробеніуса. Заданий характеристичний поліном з коефіцієнтами
також записана у формі
Фробеніуса. Заданий характеристичний поліном з коефіцієнтами ![]() є характеристичним поліномом
є характеристичним поліномом ![]() , то отримаємо систему:
, то отримаємо систему:
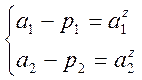
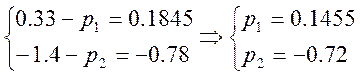
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.