За моделями , знайденими за варіантами завдання 2 з таблиці 4, побудувати моделі з простором станів. Перевести систему зі стану Х0 у стан Х=0 (таблиця 6) за мінімальну кількість моментів часу.
|
Варіант |
Початковий стан Х0* |
|
10 |
(6,6,2) |
Вважаємо систему повністю спостережуваною та повністю керованою:
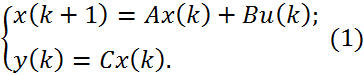
Необхідно знайти ![]() для
для ![]() та
та ![]() .
.
Для
спостережуваних систем розв’язок першого з рівнянь з системи ![]() має вигляд:
має вигляд:
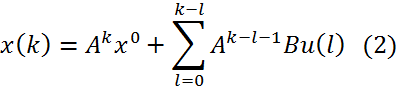
При ![]() маємо
маємо ![]()
Треба знайти
момент часу ![]() такий, що стан системи
такий, що стан системи ![]() . Рівняння
. Рівняння ![]() перепишемо у вигляді:
перепишемо у вигляді:
![]()
Це система
лінійних алгебраїчних рівнянь відносно ![]() , де
, де 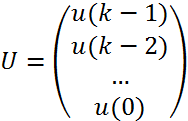 .
.
Систему ![]() можна записати в матричному вигляді:
можна записати в матричному вигляді:
![]()
Будемо вважати,
що в моделі ![]() матриці мають такі розміри:
матриці мають такі розміри: ![]() ,
, ![]() ,
, ![]() .
.
Система лінійних
рівнянь (4) має єдиний розв’язок за умови ![]() для матриці
для матриці ![]() .
.
Умова повної
керованості системою визначається як ![]() , що і забезпечить існування
одного розв’язку системи (4).
, що і забезпечить існування
одного розв’язку системи (4).
Зробимо заміну ![]() , тоді
, тоді ![]() набуде вигляду
набуде вигляду
![]()
Звідси ![]()
При ![]() маємо
маємо ![]() . Якщо
. Якщо ![]() .
.
Розглянемо задачу, коли вхід в систему має скалярний характер:
![]()
Розглянемо 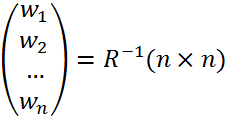 .
.
За визначенням:
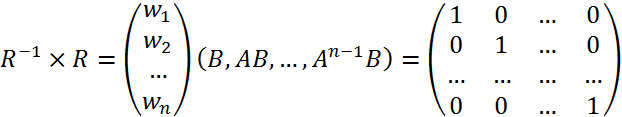
![]()
![]()
![]() . Тобто:
. Тобто:
![]() ,
, ![]()
![]()
Оскільки![]() , то, помноживши цю рівність
зліва на
, то, помноживши цю рівність
зліва на ![]() , отримаємо
, отримаємо
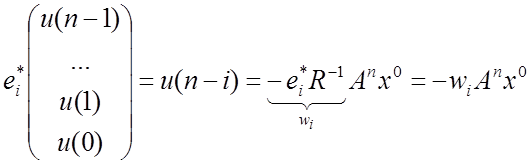 .
.
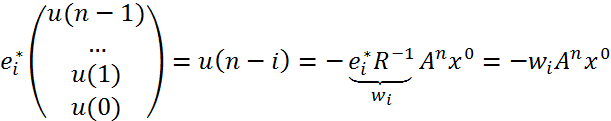
Керування
системою повинно відбуватися за законом ![]() .
.
Стверджується, що
керування ![]() переводить будь-який
початковий стан
переводить будь-який
початковий стан ![]() в стан
в стан ![]() за
за ![]() кроків.
кроків.
Практична реалізація
Дискретна лінійна модель вхід – вихід має вигляд:
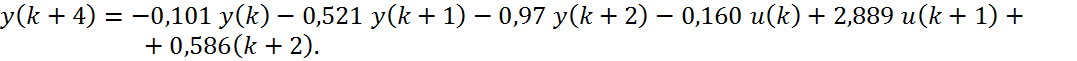
Дискретна стаціонарна лінійна детермінована модель із простором станів має вигляд:
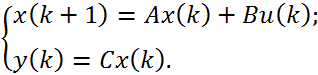
Еквівалентна модель із простором станів може бути задана матрицями:
![]() =Fb(
=Fb(![]() );
);
![]()
![]()
Використовуючи коефіцієнти заданої моделі вхід-вихід, будуємо:
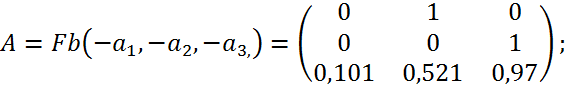
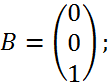
![]()
Оскільки ![]() :
:
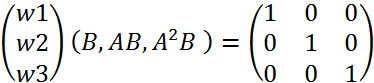
![]()
![]()
> with(LinearAlgebra):
> A:=<<0|1|0>,<0|0|1>,<0.101|0.521|0.97>>;

> B:=<0,0,1>;
>
>
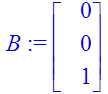
> C:=<-0.160|2.889|0.586>;
![]()
> R:=<B|A.B|A.A.B>;

> W3:=<1|0|0>;
![]()
> W3R:=W3.R;
![]()
> X[0]:=<6,6,2>;
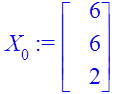
> for i from 0 by 1 to 2 do
> U[i]:=-W3.A.A.A.X[i]:
> X[i+1]:=A.X[i]+B.U[i]:
> end;
>
>
>
![]()
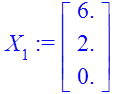
![]()
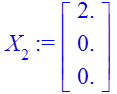
![]()
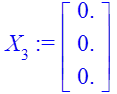
>
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.