Завдання №8
Побудувати систему зі зворотним зв’язком . Використати модальне керування з роботи №7 та за тими ж вихідними даними побудувати модальний естиматор.
|
Варіант |
Заданий спектр |
Спектр матриці А |
|
№9 |
|
|
Розв’язок
Маємо дискретну, лінійну, детерміновану, стаціонарну, динамічну модель з простором станів:
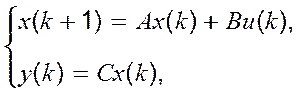 (1)
(1)
Було отримане модальне керування
керування нашої системи (1) в вигляді ![]() , де матриця
, де матриця ![]() має вигляд
має вигляд ![]() . Вона є добутком матриць
. Вона є добутком матриць 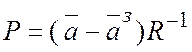 ,
, ![]() ,
,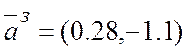 - коефіцієнти
характеристичних поліномів відповідно
- коефіцієнти
характеристичних поліномів відповідно ![]() і
і ![]() , а матриця
, а матриця ![]() . Побудуємо систему у якій
буде відбуватися наближене оцінювання
. Побудуємо систему у якій
буде відбуватися наближене оцінювання ![]() станів нашої системи, тобто в якій
отримуються оцінки
станів нашої системи, тобто в якій
отримуються оцінки ![]() . Ця система називається естиматором.
. Ця система називається естиматором.
Необхідна оцінка стану в наступний
момент часу шукається як функція від відомих входів, виходів і оцінок стану в
попередній момент часу: ![]() Оскільки модальне керування нашої системи лінійне, то
Оскільки модальне керування нашої системи лінійне, то ![]() . Матриці
. Матриці![]() ,
,![]() ,
,![]() такі, що
такі, що ![]() (*).
(*).
Для забезпечення умови (*) необхідно
щоб ![]() ,
, ![]() і власні значення
і власні значення ![]() за модулем були менше 1.
за модулем були менше 1.
> restart;with(linalg):
Warning, the protected names norm and trace have been redefined and unprotected
> a1_r:=0.2425;a2_r:=-0.4;
![]()
![]()
> a1:=0.28;a2:=-1.1;
![]()
![]()
> A:=matrix(2,2,[0,1,-a1,-a2]);
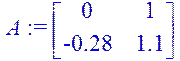
> fi2:=diag(1,1);Ia2:=band([a2],2);
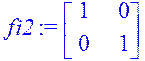
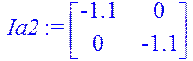
> fi1:=evalm(A&*fi2+Ia2);
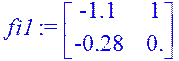
> C:=Matrix(1,2,[1,0]);
![]()
> rl1:=evalm(C&*fi1);rl2:=evalm(C&*fi2);
![]()
![]()
> RL:=stackmatrix(rl1,rl2);
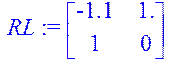
> l1_:=a1_r-a1;l2_:=a2_r-a2;L_:=transpose(matrix(1,2,[l1_,l2_]));
![]()
![]()
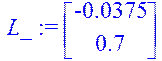
> RL1:=inverse(RL);L:=evalm(RL1&*L_);
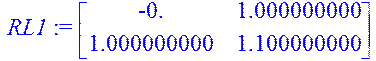
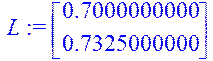
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.