Лабораторна робота №3
ст. гр.. ІН-52
Третяк Олени
Задана дискретна лінійна стаціонарна детермінована математична модель з простором станів
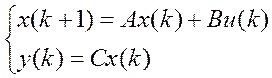
з
матрицями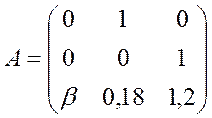 
, 
, 
.
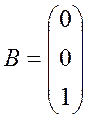Причому 
може набувати одного зі
значень елементів масиву 
, а 
- одного зі значень 
. Вважаючи початковим стан системи
,
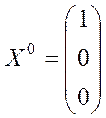розрахувати перехідні частини процесів 
та 
та
побудувати їх графіки при заданих значеннях скалярного входу:
1) 
,
де 
.
2) 
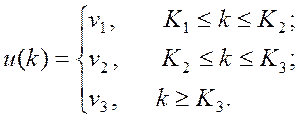
Тут К1=0; К2=Nв+2
К3=40;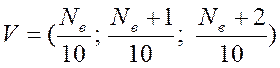 
, де 
- номер варіанта.
(в моєму випадку К2=17; V=(1,7; 1,8; 1,9) )
> restart;
> with(LinearAlgebra):
> with(stats[statplots]):
> N:=150:
> A:=<<0|1|0>,<0|0|1>,<-0.4|0.18|1.2>>:
> C:=<-2|1|-1>:
> B:=<0,0,1>:
> P:=<0.0015|-0.01|0.005>:
> x:=<1,0,0>:
> x1:=array(0..N):
> x2:=array(0..N):
> x3:=array(0..N):
> y1:=array(0..N):
> II:=array(0..N):
> for i from 0 by 1 to N do
> x1[i]:=Vector(x)[1]:
> x2[i]:=Vector(x)[2]:
> x3[i]:=Vector(x)[3]:
> M:=Multiply(A,x):
> U:=DotProduct(P,x):
> L:=ScalarMultiply(B,U):
> x:=Add(M,L):
> y:=Multiply(C,x):
> y1[i]:=y:
> II[i]:=i:
> end do:
> printf(" I x1 x2 x3 y \n"):
I x1 x2 x3 y
> for i from 1 by 1 to 150 do
> printf(" %2.0f %2.4f %2.4f %2.4f |%2.4f\n",II[i],x1[i],x2[i],x3[i],y1[i]):
>
> end do:
1 0.0000 0.0000 -0.3985 |0.0817
2 0.0000 -0.3985 -0.4802 |0.9632
3 -0.3985 -0.4802 -0.6464 |1.0157
4 -0.4802 -0.6464 -0.7017 |1.3551
5 -0.6464 -0.7017 -0.7641 |1.4218
6 -0.7017 -0.7641 -0.7824 |1.5388
7 -0.7641 -0.7824 -0.7931 |1.5560
8 -0.7824 -0.7931 -0.7842 |1.5700
9 -0.7931 -0.7842 -0.7680 |1.5431
-------------------------------------------------------------------------------
112 -0.0001 -0.0001 -0.0001 |0.0002
113 -0.0001 -0.0001 -0.0001 |0.0002
114 -0.0001 -0.0001 -0.0001 |0.0002
115 -0.0001 -0.0001 -0.0001 |0.0002
116 -0.0001 -0.0001 -0.0001 |0.0002
117 -0.0001 -0.0001 -0.0001 |0.0002
118 -0.0001 -0.0001 -0.0001 |0.0001
119 -0.0001 -0.0001 -0.0001 |0.0001
120 -0.0001 -0.0001 -0.0001 |0.0001
121 -0.0001 -0.0001 -0.0000 |0.0001
122 -0.0001 -0.0000 -0.0000 |0.0001
123 -0.0000 -0.0000 -0.0000 |0.0001
124 -0.0000 -0.0000 -0.0000 |0.0001
125 -0.0000 -0.0000 -0.0000 |0.0001
126 -0.0000 -0.0000 -0.0000 |0.0001
127 -0.0000 -0.0000 -0.0000 |0.0001
128 -0.0000 -0.0000 -0.0000 |0.0001
129 -0.0000 -0.0000 -0.0000 |0.0001
130 -0.0000 -0.0000 -0.0000 |0.0000
131 -0.0000 -0.0000 -0.0000 |0.0000
132 -0.0000 -0.0000 -0.0000 |0.0000
133 -0.0000 -0.0000 -0.0000 |0.0000
134 -0.0000 -0.0000 -0.0000 |0.0000
135 -0.0000 -0.0000 -0.0000 |0.0000
> a1:=convert(x1,'list'):
> b1:=convert(x2,'list'):
> c1:=convert(x3,'list'):
> d1:=convert(y1,'list'):
> oo:=convert(II,'list'):
> plots[display](scatterplot(oo,a1,color=red) );
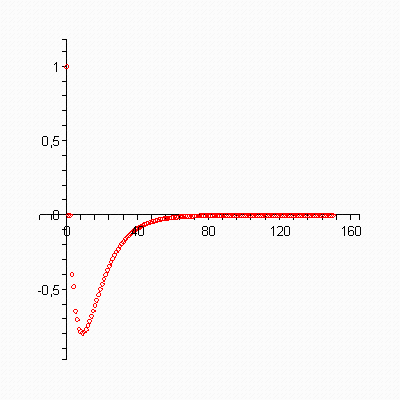
> plots[display](scatterplot(oo,b1,color=red) ); > plots[display](scatterplot(oo,c1,color=red) );
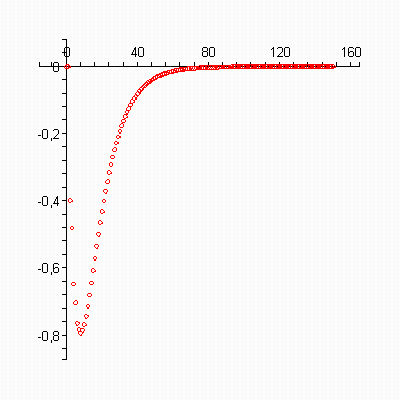
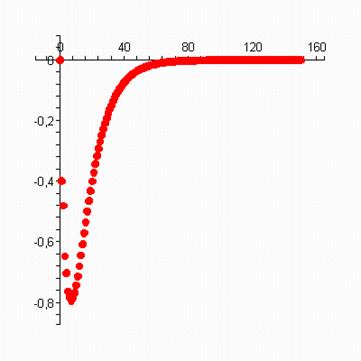
> plots[display](scatterplot(oo,d1,color=red) );
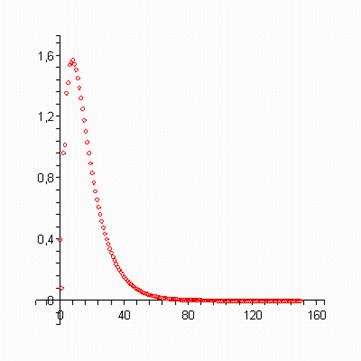
> restart;
> with(stats[statplots]):
> with(LinearAlgebra):
> N:=120:
> x1:=array(0..N):
> x2:=array(0..N):
> x3:=array(0..N):
> y1:=array(0..N):
> UU:=array(0..N):
> A:=<<0|1|0>,<0|0|1>,<-0.4|0.18|1.2>>:
> C:=<-2|1|-1>:
> B:=<0,0,1>:
> x:=<1,0,0>:
> for i from 0 by 1 to N do
> if (i<=17) then U:=1.7
> elif (i>17) and (i<=40) then U:=1.8
> else U:=1.9
> end if:
> x1[i]:=Vector(x)[1]:
> x2[i]:=Vector(x)[2]:
> x3[i]:=Vector(x)[3]:
> M:=Multiply(A,x):
> L:=ScalarMultiply(B,U):
> x:=Add(M,L):
> y:=Multiply(C,x):
> y1[i]:=y:
> II[i]:=i:
> UU[i]:=U:
> end do:
> #printf(" Vivid znacheniy \n "):
> #printf(" I x1 x2 x3 y \n"):
> for i from 0 by 1 to 120 do
> #printf(" %2.4f %2.4f\n",II[i],UU[i]);
> printf(" %2.0f %2.4f %2.4f %2.4f |%2.4f\n",II[i],x1[i],x2[i],x3[i],y1[i]):
> end do:
0 94.9616 94.9641 94.9664 |-189.7304
1 94.9641 94.9664 94.7686 |-189.6949
2 94.9664 94.7686 94.5307 |-189.2152
3 94.7686 94.5307 94.2086 |-188.7111
4 94.5307 94.2086 93.8584 |-188.0341
5 94.2086 93.8584 93.4753 |-187.3229
6 93.8584 93.4753 93.0815 |-186.5492
7 93.4753 93.0815 92.6800 |-185.7634
8 93.0815 92.6800 92.2805 |-184.9658
9 92.6800 92.2805 91.8864 |-184.1768
------------------------------------------------------------------------------
102 94.8619 94.8709 94.8793 |-189.7497
103 94.8709 94.8793 94.8872 |-189.7660
104 94.8793 94.8872 94.8945 |-189.7812
105 94.8872 94.8945 94.9014 |-189.7955
106 94.8945 94.9014 94.9078 |-189.8088
107 94.9014 94.9078 94.9138 |-189.8213
108 94.9078 94.9138 94.9194 |-189.8329
109 94.9138 94.9194 94.9247 |-189.8438
110 94.9194 94.9247 94.9296 |-189.8540
111 94.9247 94.9296 94.9342 |-189.8635
112 94.9296 94.9342 94.9385 |-189.8724
113 94.9342 94.9385 94.9425 |-189.8807
114 94.9385 94.9425 94.9462 |-189.8885
115 94.9425 94.9462 94.9497 |-189.8957
116 94.9462 94.9497 94.9530 |-189.9025
117 94.9497 94.9530 94.9561 |-189.9089
118 94.9530 94.9561 94.9589 |-189.9148
119 94.9561 94.9589 94.9616 |-189.9204
120 94.9589 94.9616 94.9641 |-189.9256
> a1:=convert(x1,'list'):
> b1:=convert(x2,'list'):
> c1:=convert(x3,'list'):
> d1:=convert(y1,'list'):
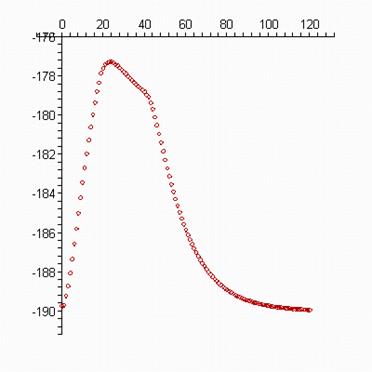
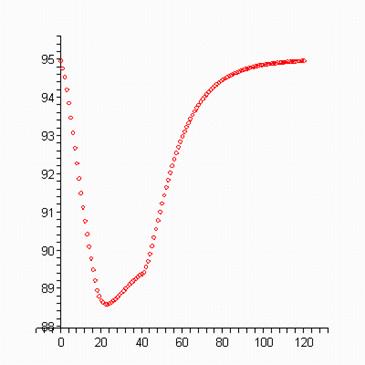
> oo:=convert(II,'list'):
> plots[display](scatterplot(oo,a1,color=red) ); > plots[display](scatterplot(oo,b1,color=red) );
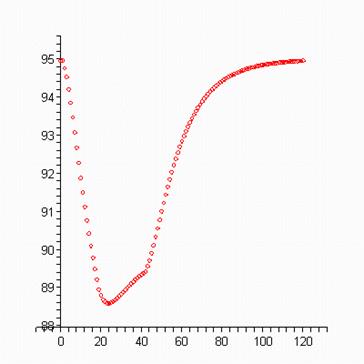
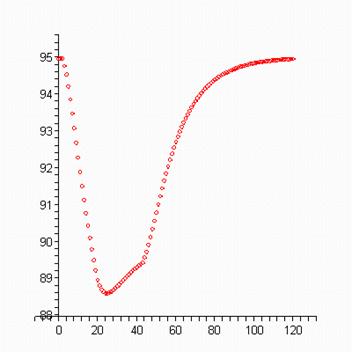
> plots[display](scatterplot(oo,c1,color=red) ); > plots[display](scatterplot(oo,d1,color=red) );
 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
