Тестові питання на 4 бали з курсу "Теорія систем та математичне моделювання"

Питання на „4 ” з курсу „Теорія систем та мат. мод.”(Назаренко)

№ 1.

Для системи N=8 разів реєструються вхідні впливи на систему  і відповідні їм вихідні значення . Побудувати дискретну лінійну модель вхід-вихід другого порядку.

 у(к+2)=-0.6у(к)-0.2у(к+1)+1.6u(к)+0.8u(к+1);

№2

Нехай існує модель вхід-вихід

y(k)+2y(k+1)-y(k+2)+y(k+3)=0.5u₁(k)–0.2u₁(k+1)+u₂(k+1)–4u₂(k+2).

Тоді матриці А, В і С еквівалентної моделі з простором станів мають вигляд:

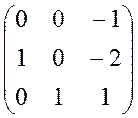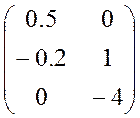A= , B = , C = (0, 0, 1);

№3

За відомою моделлю вхід-вихід

у(к+2)=-0.6у(к)-0.2у(к+1)+1.6u(к)+0.8u(к+1) побудувати модель з простором станів.

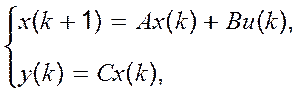
A=Fb(-a₁, -a₂), В=е₂і С=(c₁,c₂).

      .

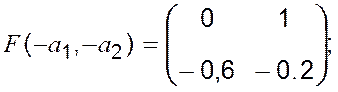
№4

Перевірити на керованість систему, модель якої має вигляд

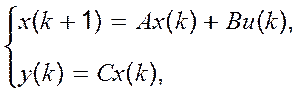
де 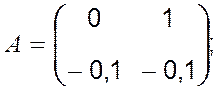 , визначивши значення відповідного критерію

Решение

За умовою повної керованості ––  критерієм Калмана:

rg(B, АВ,..., А^n-1B) = n.

Для нашої задачі система керована, якщо rg(B,АВ)= 2. Перевіримо це

, .

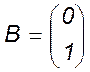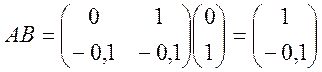Ранг матриці rg(B,АВ)=rg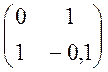=2, оскільки визначник її не дорівнює нулю.

Ответ  rg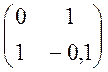=2;.

№5

Визначити значення критерію  на повну спостережуваність системи

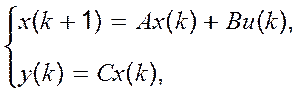
де       .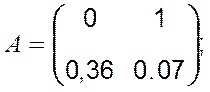

Решение

У нашому випадку треба перевірити rg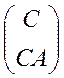=2. Дійсно, , .

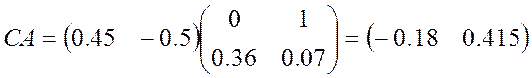Ранг матриці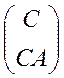 rg= rg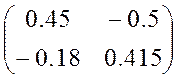=2, оскільки очевидно, що визначник її не дорівнює нулю.

rg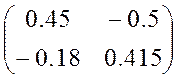=2,

№6

За математичною моделлю об'єкта керування у формі системи диференціальних рівнянь визначити його передатну матрицю .

Лінійна неперервна модель досліджуваного об’єкта має вигляд

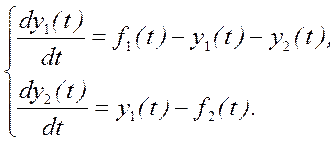
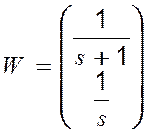
№7

Визначити значення критерію стійкості  системи

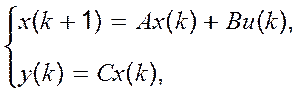
з матрицею .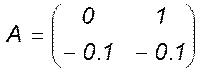

Решение

Розв’язання. Побудуємо її характеристичний поліном за формулою

,

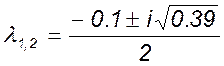
№8

Досліджувана система представлена моделлю з простором станів

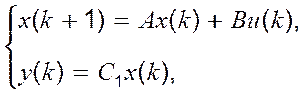,  де ,.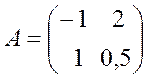

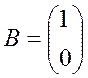          Необхідно побудувати керування за заданим спектром

№9 Для матриці А визначити подібні матриці Фробеніуса та Жордана

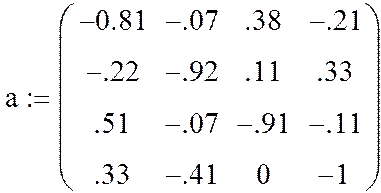
> A:=<<-0.81|-0.07|0.38|-0.21>,<-0.22|-0.92|0.11|0.33>, <0.51|-0.07|-0.91|-0.11>,<0.33|-0.41|0|-1>>;

> FrobeniusForm(A);

> TFb=Transpose(Fb);

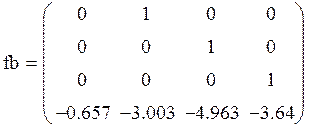
> Xa:=CharacteristicPolynomial(A,x);

> Specter:=solve(Xa);

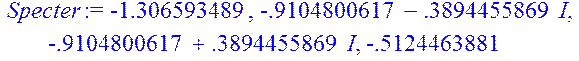
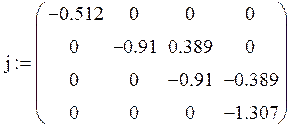
№10

Побудувати неперервну математичну модель вхід-вихід за даними вхід-вихідного експерименту значень входів у систему  та її реакцій .

U={11,2 12,6  18,6  21,4  25  29,6   31,1  38,2  40}

Y={0,99  0,74  0,69  0,58  0,41 0,33 0,26  0,19 0,1}

+а) Y= 2.458-0.63*Ln(u);

№11.

Властивість математичної моделі, що відбиває ступінь збігу передвіщених з її допомогою значень параметрів об'єкта з істинними значеннями цих параметрів..

точність

№12.

Побудувати неперервну математичну модель вхід-вихід за даними вхід-вихідного експерименту значень входів у систему  та її реакцій .

U={0,1  0,5  1,05   2,2  3,65  5,5  7,85  9,45 14,75}

Y={10  9,33  8,67  7,33  6,6  4,65  3,34  2,65  1,34}

№13.

Побудувати дискретну лінійну модель вхід – вихід третього порядку за показниками входів у систему  та її реакцій , що вимірювалися в однакові моменти часу 10 разів.

U={1, 0, 2, -1, -1, 3, 2, 1, 0, 1}

Y={2,2;0,98;1,17;2,81;2,2;-1,2;0,9;-2,2;2,3;1,1}

Ответ

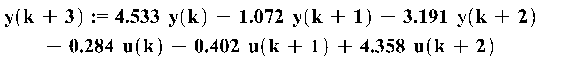
№14.

Побудувати модальне керування для системи

 

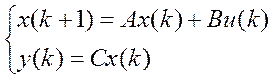
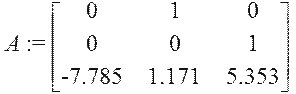
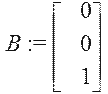
за заданим спектром

Решение

Сперва составляем характеристическое уравнение и нахожим заданные коефициенты а1 а2 а3

A+BP, где Р=(р1,р2,р3)

Пример

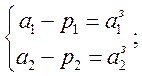
Ответ: Р=(8,315; -2,631; -4,053)

№15. Проблема представлення або ідентифікації системи: - Створення математичної моделі

№16. Проблема спостережуваності системи:

Можливість оцінити станис ситеми за відомими значеннями входів і виходів

№17. Проблема керованості системи:

Визначення таких входів, що б дозволили отримати очікувані виходи

№18.

За умовою повної керованості ––  критерієм Калмана система

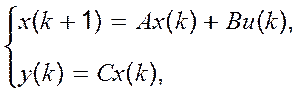, де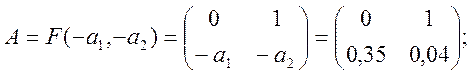

.

керована, якщо:

якщо

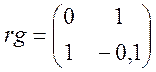=2 

система керована

№19 Досліджувана система представлена моделлю з простором станів

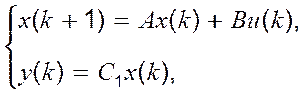,  де А= Fb, , .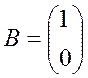

Спектр матриці А:

  Решение

А= Fb=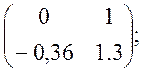

№20

Система, модель якої має вигляд

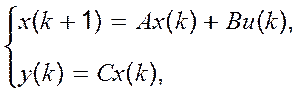         де А=  , .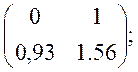

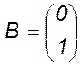 повністю спостережувана, якщо …

Для нашого випадку маємо таку умову:

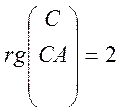
=2

система спостережувана