За моделлю вхід-вихід:
Y(K+4)
=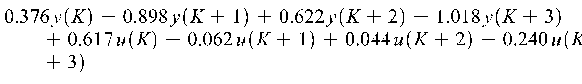
побудувати еквівалентну модель з простором станів.
Вважаючи початковим стан системи
X1:=[colum](1,0,0,0);
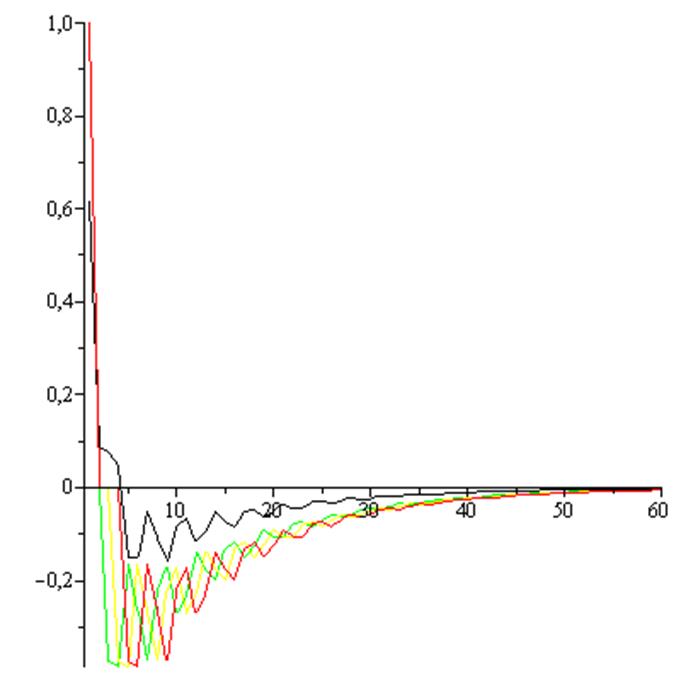
розрахувати
перехідні частини процесів ![]() та
та
![]() та побудувати їх
графіки при заданих значеннях скалярного входу:
та побудувати їх
графіки при заданих значеннях скалярного входу:
1) ![]() ,
,
де ![]() ;
;
2) 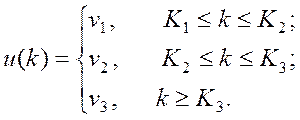
Тут К1=0; К2=Nв+2 К3=40;
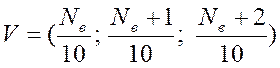 , де
, де ![]() - номер варіанта.
- номер варіанта.
Математичне обґрунтування алгоритму розв’язку
Дискретна стаціонарна лінійна детермінована динамічна модель з простором станів має вигляд:
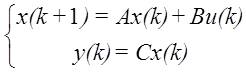 (1)
(1)
де
![]()
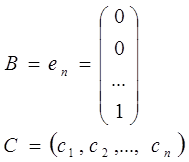
![]() (2)
(2)
- модель вхід-вихід
Модель 1 це система різницевих рівнянь записаних в матричному вигляді. Для її розв’язку, тобто для визначення станів системи x(k) та виходів y(k) при k=1,2,… ,необхідно знайти відповідне значення входів та початковий стан системи, за цих умов система завжди має розв’язок.
Моделі 1 та 2 являються еквівалентними.
Доведемо еквівалентність моделей 1 та 2.
Спочатку доведемо рівності:
φj (Fb(-a1, ..., -an ))en =еj для j=1,...,n, (3)
де φj(λ) - похідні поліноми матриці Фробеніуса Fb(-a) .
1. База
індукції. Для j=n
маємо ![]() ,
тобто (2) виконано.
,
тобто (2) виконано.
2. Передбачення індукції. Нехай (3) справедливо для j=n-1, n-2, …, l+1.
Доведемо справедливість твердження для j=l:
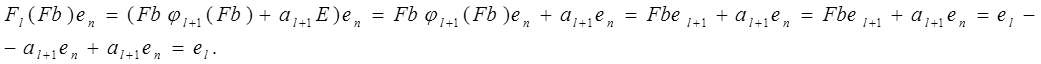
Для доведення
еквівалентності моделей врахуємо, що характеристичний поліном матриці А
буде мати вигляд ![]()
Для
еквівалентності моделей треба довести, що ![]()
Іншу модель з
простором станів, яка буде еквівалентною до моделі (1),
можна отримати, взявши ![]()
Покажемо, як від моделі (1) можна перейти до моделі (2).
Маємо
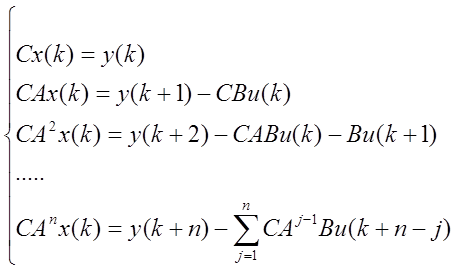 (4)
(4)
Система (4) містить n+1 рівняння. Помножимо від 1-го до n-го рівняння на відповідні коефіцієнти характеристичного полінома матриці А і додамо отримані в результаті множення перші n рівнянь до останнього, n+1 у системі (4).
Практична реалізація
#Alexandr Opara
#alexandr.opara@gmail.com
#Varian 13
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()

![]()
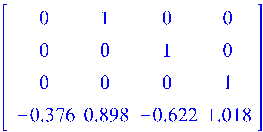
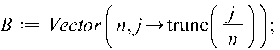
![]()
![]()
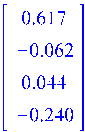
#part1
![]()
![]()


![]()
![]()
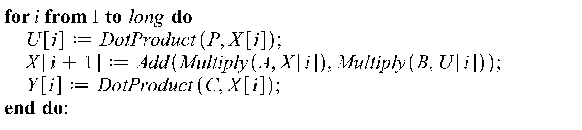
![]()
![]()
![]()
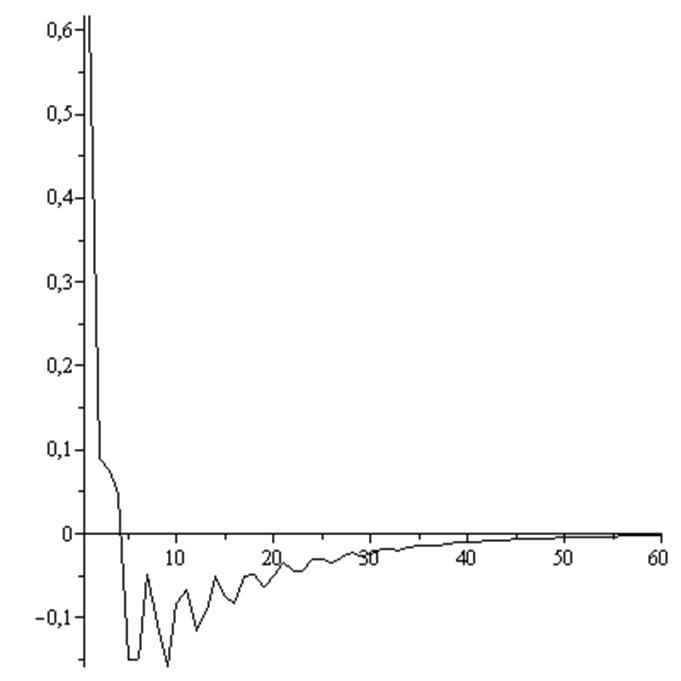
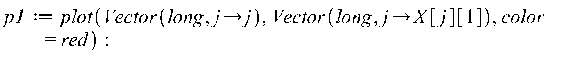
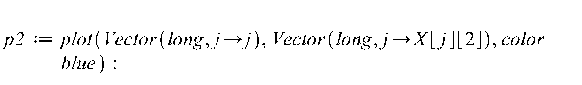
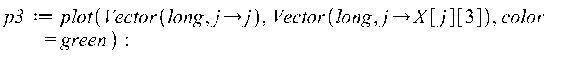
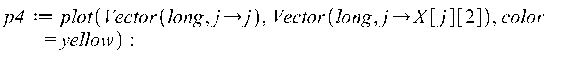
![]()
![]()
![]()
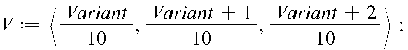
![]()
![]()


![]()
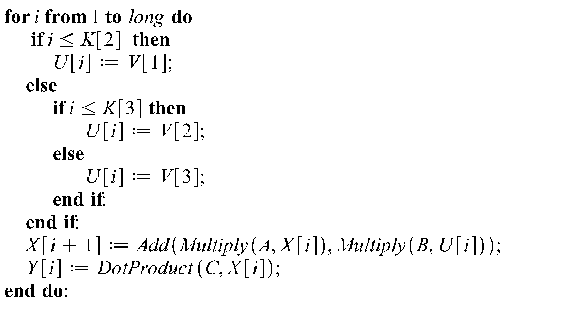
![]()
![]()
![]()
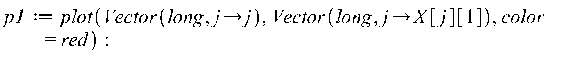
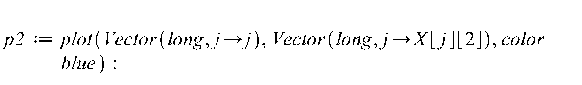
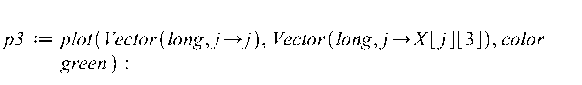
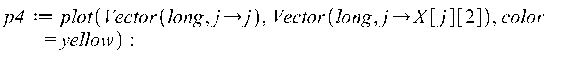
![]()
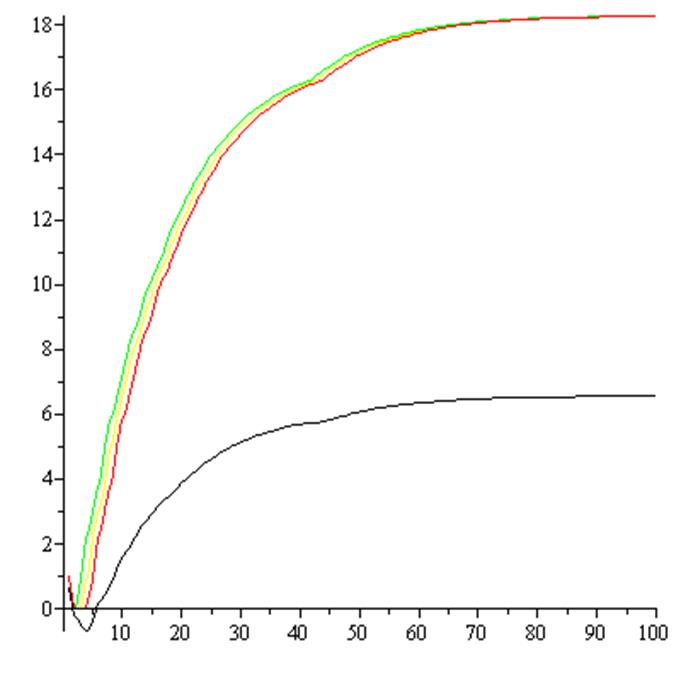
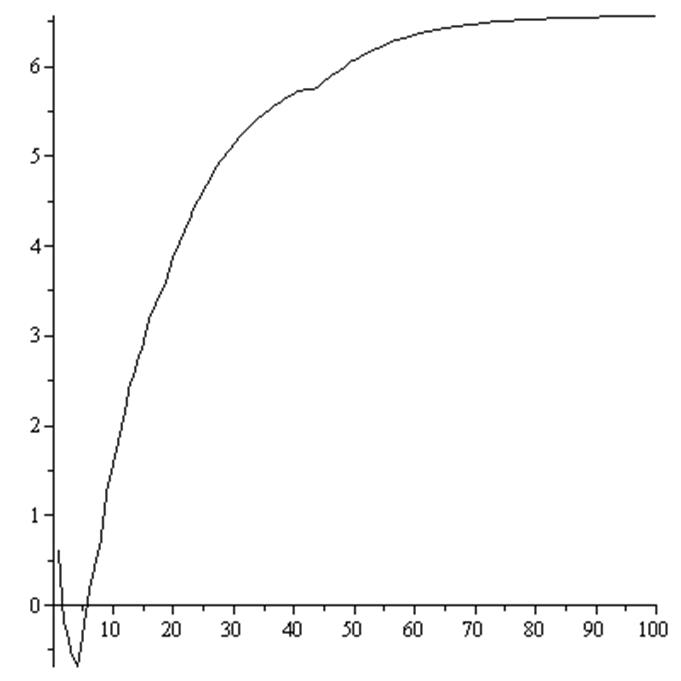
Висновок: Система є стійною.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.