Лабораторна робота №2
з теорії систем
студента ММФ групи ПМ-61/1
Чепульського Сергія
Завдання Побудувати дискретну лінійну модель вхід – вихід за показниками входів
у систему ![]() та її реакцій
та її реакцій ![]() , що
вимірювалися в однакові моменти часу.
, що
вимірювалися в однакові моменти часу.
|
3 |
U={-1.4; -1.2; -1; -0.7; -0.4; 0.08; 0.57; 0.99;1.26; 1.3; 1.15; 0.87; 0.5} Y={-0.56; -0.95;-1.26;-1.414; -1.32; -0.96;-0.41;0.186;0.696;1.01;1.16;1.2;1.2} |
Розв’язання:
Для системи N=13 разів реєструються вхідні впливи на систему U={-1.4; -1.2; -1; -0.7; -0.4; 0.08; 0.57; 0.99;1.26; 1.3; 1.15; 0.87; 0.5} і відповідні їм вихідні значення Y={-0.56; -0.95;-1.26;-1.414; -1.32; -0.96;-0.41;0.186;0.696;1.01;1.16;1.2;1.2}.
Виберемо порядок
моделі ![]() . Тоді вона набуде вигляду
. Тоді вона набуде вигляду ![]() . Використовувати її можна для
. Використовувати її можна для ![]() , щоб спрогнозувати відповідні відомі
значення реакції системи. При
, щоб спрогнозувати відповідні відомі
значення реакції системи. При
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() .
.
Система похибок має вигляд:
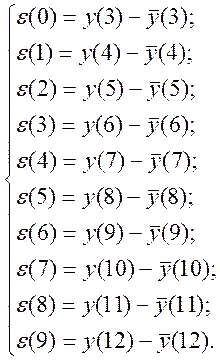
Якщо її записати в матричному вигляді,
одержимо ![]() . Невідомий вектор
. Невідомий вектор  знаходимо,
розв’язуючи систему лінійних алгебраїчних рівнянь
знаходимо,
розв’язуючи систему лінійних алгебраїчних рівнянь ![]()
Тут матриці мають вигляд
![]()
![]() ...
... ![]()
![]() …
… ![]()
![]()
![]() ...
... ![]()
![]() ...
... ![]()
R= ………………………………..…………..….....
![]() ...
... ![]()
![]() …
…![]()
і вектор ![]()
![]() .
.
Реалізація в Maple11:
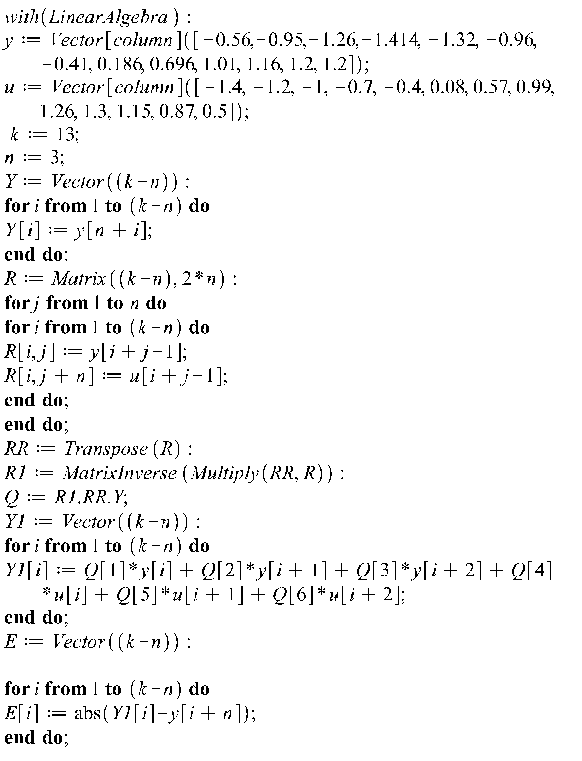


![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.