Лабораторна робота №2
Сидоренко Олега
ПМ-71
Варіант №11
Побудувати дискретну лінійну модель вхід –
вихід за показниками входів у систему ![]() та її
реакцій
та її
реакцій ![]() , що вимірювалися в однакові моменти часу
, що вимірювалися в однакові моменти часу ![]() разів:
разів:
|
Варіант |
Значення вхід-вихідних експериментів |
|
|
11 |
U={0;0.025;0.0062;0.016;0.039;0.097;0.244;0.61; 1.52; 3.8; 9.53; 23.8; 59.6; 149.0} Y={3.2*10-6;4.8*10-6;6.9*10-6;9.8*10-6;1.3*10-5;1.9*10-5; 2.6*10-5; 3.6*10-5; 5*10-5;7*10-5;1*10-4;1.5*10-4; 2.5*10-4; 4.8*10-4} |
|
Нехай задано результати N експериментів з
входами ![]() та виходами
та виходами ![]() .
.
Будемо шукати лінійну математичну модель, яка у середньоквадратичному змісті найкращим способом відтворює отримані дослідні дані. Зафіксуємо n і будемо шукати вхід-вихід модель вигляду:
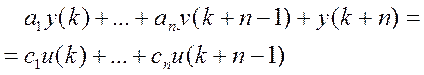
Це означає, що необхідно знайти коефіцієнти a1,…an, c1,…cn рівняння.
Якщо yM(k)-вихід, який
обчислюється за моделлю і відповідає входу u(k), то величину 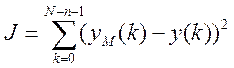 будемо розглядати як міру відхилення
дійсного закону поведінки процесу від математичної моделі.
будемо розглядати як міру відхилення
дійсного закону поведінки процесу від математичної моделі.
Порядок моделі n визначає кількість попередніх моментів часу, що впливають на реакцію системи в поточний момент. Обраний порядок моделі має задовольняти умову 2n+1<=N.
Перепишемо модель вхід-вихід у вигляді:
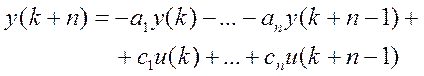
і введемо позначення:
![]()
![]() =
col(-a1,…,-an, c1,… cn).
=
col(-a1,…,-an, c1,… cn).
Задача зводиться до знаходження такого значення
векторного параметра ![]() , яке мінімізує
середньоквадратичну похибку:
, яке мінімізує
середньоквадратичну похибку:
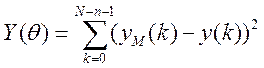
Дана система похибок може бути представлена у
матричному вигляді. У результаті одержимо СЛАР, розв’язком якої і буде шуканий
вектор ![]() :
:
![]() , де
, де
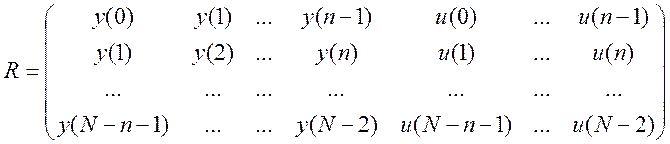
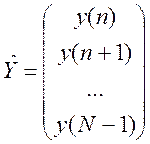 .
.
Виконати дане завдання можна використовуючи різні пакетні програми. Наприклад, досить легко виконати його, використовуючи бібліотеку лінійної алгебри пакету Maple. Використання стандартних функцій цього пакету дозволяє визначити коефіцієнти, необхідні для побудови моделі вхід-вихід:
> with(linalg):
> R:=linalg[matrix](11,6,[3.2e-6,4.8e-6,6.9e-6,0,0.025,0.0062,4.8e-6,6.9e-6,9.8e-6,0.025,0.0062,0.016,6.9e-6,9.8e-6,1.3e-5,0.0062,0.016,0.039,9.8e-6,1.3e-5,1.9e-5,0.016,0.039,0.097,1.3e-5,1.9e-5,2.6e-5,0.039,0.097,0.244,1.9e-5,2.6e-5,3.6e-5,0.097,0.244,0.61,2.6e-5,3.6e-5,5e-5,0.244,0.61,1.52,3.6e-5,5e-5,7e-5,0.61,1.52,3.8,5e-5,7e-5,1e-4,1.52,3.8,9.53,7e-5,1e-4,1.5e-4,3.8,9.53,23.8,1e-4,1.5e-4,2.5e-4,9.53,23.8,59.6]);
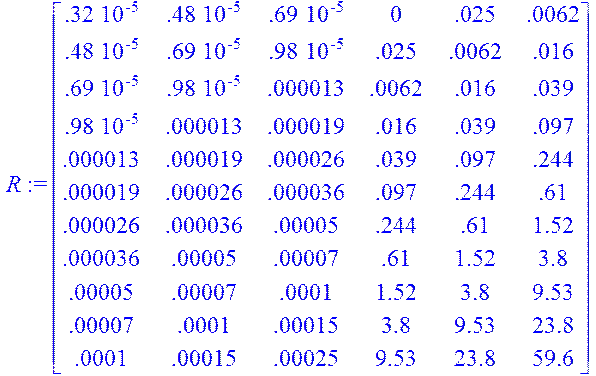
> Y:=linalg[matrix](11,1,[9.8e-6,1.3e-5,1.9e-5,2.6e-5,3.6e-5,5e-5,7e-5,1e-4,1.5e-4,2.5e-4,4.8e-4]);
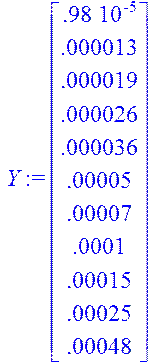
> RR:=linalg[transpose](R);

> YY:=linalg[transpose](Y);
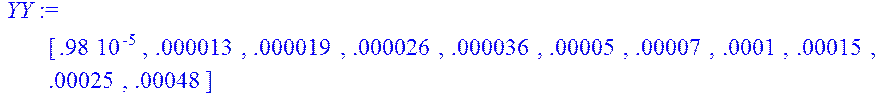
> A:=evalm(RR &* R);

> B:=evalm(RR &* Y);
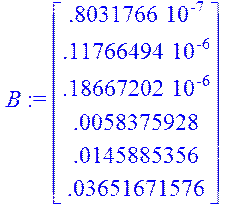
> with(LinearAlgebra):
> A1:=<<2.007893e-8|2.92205e-8|4.568702e-8|0.001325973580|0.003314179360|0.008294898340>,<2.92205e-8|4.256869e-8|6.670514e-8|0.001958888260|0.004895973580|0.01225409936>,<4.568702e-8|6.670514e-8|1.0504565e-7|0.003164535600|0.007908888260|0.01979585358>,<0.001325973580|0.001958888260|0.003164535600|108.0147854|269.9083692|675.6733598>,<0.003314179360|0.004895973580|0.007908888260|269.9083692|674.4547854|1688.388369>,<0.008294898340|0.01225409936|0.01979585358|675.6733598|1688.388369|4226.614160>>;

> AA:=MatrixInverse(A1);

> B:=<.8031766000e-7,.1176649400e-6,.1866720200e-6,.5837592800e-2,.1458853560e-1,.3651671576e>;
>
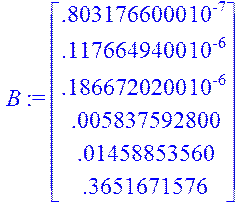
> X:=Multiply(AA,B);
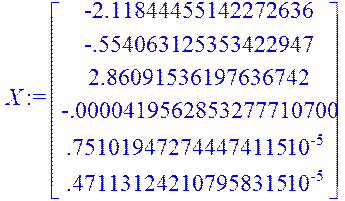
> y(k+3):=2.118*y(k)+0.5554*y(k+1)-2.86*y(k+2)-0.000042*u(k)+0.0000075*u(k+1)+0.0000047*u(k+2);
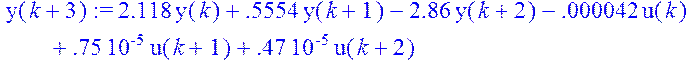
4. Висновок:
У даній лабораторній роботі було побудовано лінійну дискретну детерміновану модель вхід-вихід.
Задача була зведена до розв’язання СЛАР. Її було розв’язано за допомогою стандартних функції пакету Maple. У результаті отримали модель вхід-вихід:
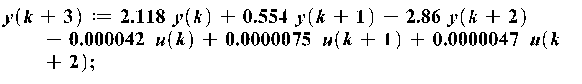
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.