Елементи алгебри матриць (Лабораторна робота № 1), страница 2

Для i=1 з (1.7) одержуємо φ₀(λ)= Х_А(λ). З визначення φ_j(λ)  випливає, що φ_j(λ)=a_j+a_j+1λ+…+a_n λ^n-j-1+λ^n-j і похідні поліноми від матричного аргументу А є такими:                           φ_n(A)=I,  φ_j-1(A) = Aφ_j (A) + a_jI,     j=n,n-1,…,2, тобто маємо Q_j = φ_j(A). Тоді (1.4) набуде вигляду

(λI-A)^-1=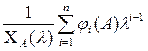 .             (1.9)

Для λ = 0 одержуємо A^-1 =– φ₁(Α)/a₁.

Якщо А_ij(λ)=сопst, для деяких i і j, тo d(λ)=1 і φ_Α(λ)=X_А(λ).

Коефіцієнти полінома Х_A(λ) можна обчислювати без розкриття визначника детермінанта det(λI-A). У прикладних задачах відомий такий вектор B, що rg(B,АВ,...,А^n-1В)=n, де n - розмірність матриці А.

Розглянемо систему лінійних алгебраїчних рівнянь

Вх₁ + АВх₂ + ··· + А^n-1 Вх_n = -АⁿВ

i покажемо, що її розв’язком є  x₁=a₁,…, х_n = a_n , де а_i - коефіцієнти X_A(λ).

За теоремою Гамільтона-Келі маємо

a₁I + a₂A +…+a_nA^n-1+Aⁿ=0.            (1.10)

Помноживши справа обидві частини рівності (1.10) на B і перенiсши в праву частину вектор АⁿВ, одержимо

Βa₁ + АВа₂ +...+ А^n-1 Ва_n = -Аⁿ В.

З однозначності розкладання вектора за лінійно незалежними B,АВ,...,А^n-1В випливає твердження.

Існує спосіб обчислення коефіцієнтів aι,a₂,...,a_n характеристичного многочлена без розв’язання системи рівнянь. Він називається методом Сур’ї-Фаддєєва і полягає в наступному.

Спочатку обчислюється a_n=-Sр(А). Потім для  i=n,n-1,…,2 мають місце рекурентні співвідношення:

φ_i-1(Α)=Aφ_i (Α) + a_iIR=Aφ_i-1(A),a_i-1=-Sp(R)/(n-i+2).             (1.11)

Цей метод дозволяє також обчислювати обернені матриці, користуючись лише операцією множення матриць.

3) матриця переходу до подібної матриці Фробеніуса

матрицяR=(φ₁(A)B,…,φ_n(Α)Β) є матрицею переходу до матриці Фробеніуса: R^-1А R=Fb.

В- стовпець (-а₁, -а₁,...,-а_п),

>  B:=<1.71,-0.62,0.89,-0.94>;

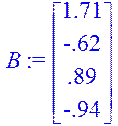
> fi4:=IdentityMatrix(4);

> A1:=AA:

>  c1:=ScalarMatrix(3.78,4);

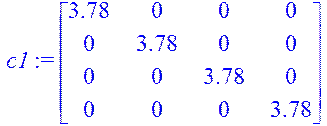
> fi3:=Add(A1,c1);

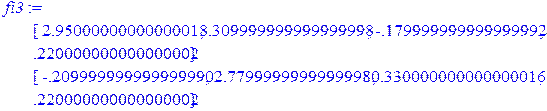
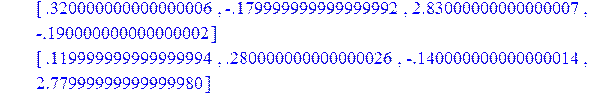
>  c2:=ScalarMatrix(5.416,4);

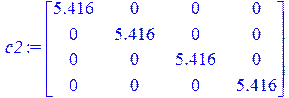
> A2:=Multiply(AA,fi3);

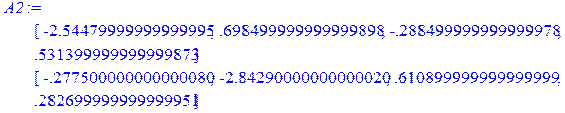
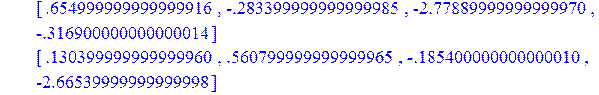
>  fi2:=Add(A2,c2);

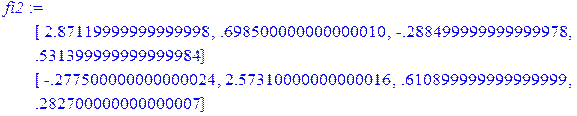
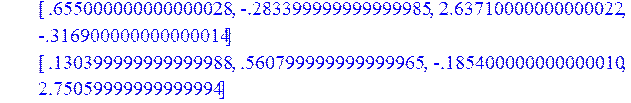
> A3:=Multiply(AA,fi2);

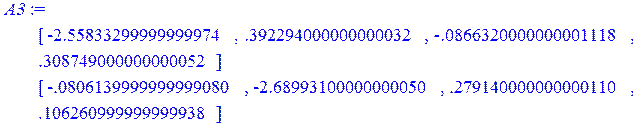
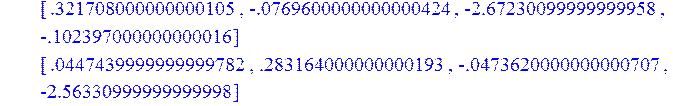
> c3:=ScalarMatrix(3.4946,4);

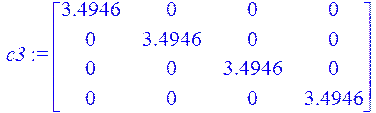
>  fi1:=Add(A3,c3);

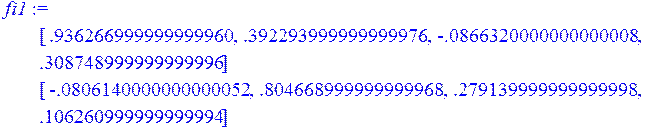
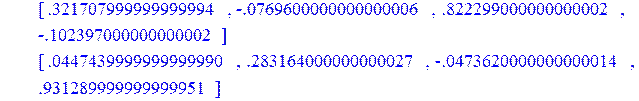
>  stb1:=Multiply(fi1,B);

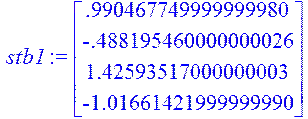
> stb2:=Multiply(fi2,B);

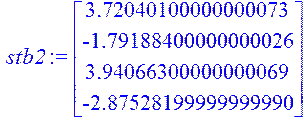
> stb3:=Multiply(fi3,B);

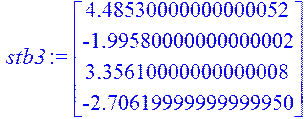
> stb4:=Multiply(fi4,B);

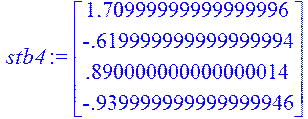
> R:=<stb1|stb2|stb3|stb4>;

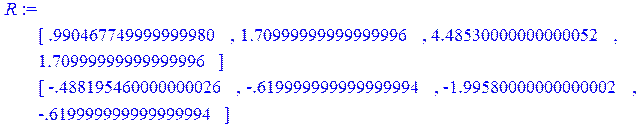
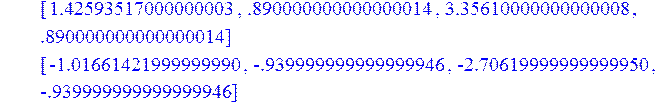
> R1 := MatrixInverse(R);

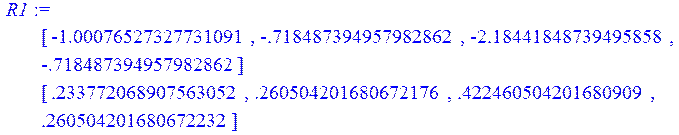
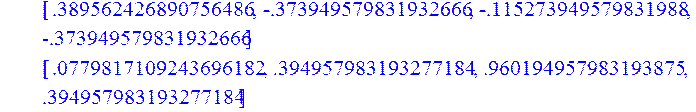
> z:=Multiply(R1,AA);

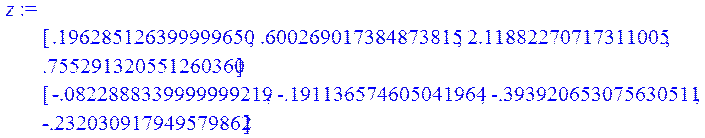
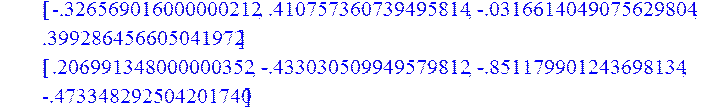
4)  подібні матриці  Фробеніуса та Жордана;

Теорема . Нехай А - довільна () – матриця і  - її  різні власні значення з геометричними  та алгебраїчними  кратностями. Тоді для кожного власного значення  існують  натуральних чисел  таких, що  а також невироджена () – матриця Т, така, що матриця  яка називається нормальною формою Жордана матриці А, має вигляд

Позначимо через I_k одиничну матрицю k-го порядкy. Блокова матриця

 

                                     A₁₁    A₁₂

                                   A₂₁     A₂₂        ,

де A₁₁=col(0,…,0), A₁₂=I_n-1, A₂₁=β₁, A₂₂=(β₂,…,β_n,,), називається матрицею Фробеніуса. Вона цілком визначається елементами нижнього рядка β=(β₁,β₂,...,β_n) і тому будемо позначати її як Fb(β).

Можна показати шляхом розкладання визначника за останнім рядком, що