XFb(β)= - β1 – β2 λ-….- βn λn-1+ λn.
Алгебраїчне доповнення елемента, що стоїть в n-му рядку і першому стовпчику матриці λI-Fb(β), дорівнює одиниці, тому характеристичний поліном матриці Фробеніуса збігається з його мінімальним поліномом.
Нехай еi - одиничний вектор, i-та координата якого дорівнює одиниці, а інші дорівнюють нулю, i=1, … , п. Тоді Fb(β)можна представити як
Fb(β)=(β1en ,e1 + β2 en,…,en-1 + βn en).
Якщо для матриці А існує такий вектор B, що rg(B,АВ,...,Аn-1В)=n, тo існує така невироджена матриця R, що R-1АR= Fb(β). У цьому випадку говорять, що матриця А може набути форми Фробеніуса.
Для доведення розглянемо похідні поліноми φ1(λ),…,φn(λ) матриці A. Оскільки
φj(A)B=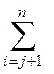 aiAi-j-1B, де an+1=1,
aiAi-j-1B, де an+1=1,
то з лінійної незалежності В,АВ,...,Аn-1В випливає лінійна незалежність векторів
φ1(Α)Β, φ2(Α)Β1, ..,φn(A)B.
Розглянемо матрицю R=(φ1(A)B,…,φn(Α)Β) і покажемо, що вона приводе матрицю А до форми Фробеніуса.
Позначимо
через ώi i-й рядок матриці R-1. Тоді
маємо ώiφj(А)B=1 для i=j і ιυίφj(Α)Β=0,
якщо i![]() j. У результаті одержимо
j. У результаті одержимо
R-1AR=сol(ώ1,…, ώn)A(φ1(A)B, φ2(A)B,…, φn(A)B)=
=col(ώ1,…, ώn)( Aφ1(A)B, Aφ2(A)B,…, Aφn(A)B)=
=col(ώ1,…, ώn)((φ0(A)-a1I)B,…,(φn-1(A)-anI)B)=
=(-a1en,e1-a2en,…,en-1-anen)=Fb(-a1,…,-an)=Fb(-a).
Отже, матриця Фробеніуса, подібна до матриці А, має елементами нижнього рядка коефіцієнти полінома ΧA(λ) з протилежними знаками і виконується R-1В=R-1φn(Α)Β=еn .
Перейдемо до розгляду матриць Грама, що, зокрема, використовуються для встановлення лінійної залежності векторів.
Нехай задані вектори-стовпці υ1,…,υm . Утворимо з них n×m-матрицю. Позначимо V=(υ1,…,υm). Матриця Г(υ1,…,υm) = V*×V називається матрицею Грама.
υ1*υ 1 υ1*υ2 …. υ1*υm
υ2*υ1 υ2*υ2 …. υ2*υm
Г(υ1,…,υm)= … … …. …….
υm*υ1 υm*υ2 …. υm*υm
Критерій Грама
лінійної незалежності векторів υ1,…,υn полягає в
тому, що detГ(υ1,…,υm)![]() 0
0
матриця Фробеніуса- це блочна матриця вигляду:
 |
A11 A12
A21 A22 ,
Де A11 – стовпець з нулів, A12 одинична матриця, -A21 -а1 ,A22 - -а2, -а3,...,-ап
> Fb:=Multiply(z,R);
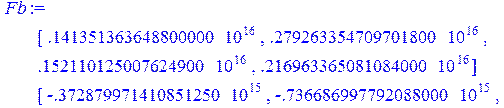
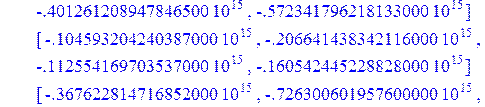
![]()
> Fb:=<<0|1|0|0>,<0|0|1|0>,<0|0|0|1>,<-0.8501|-3.4946|-5.416|-3.78>>;
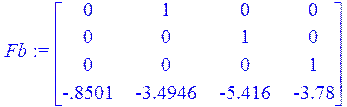
> Fb1:=FrobeniusForm(AA);
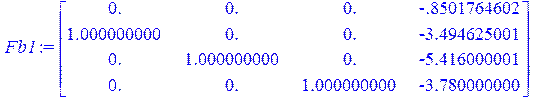
> Fb:=Transpose(Fb1);
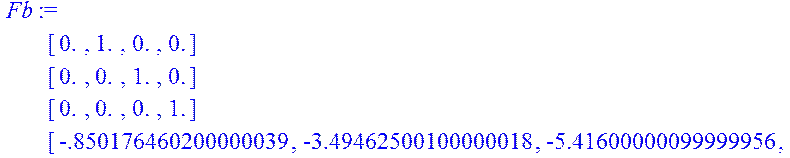
![]()
> Fb:=<<0|1|0|0>,<0|0|1|0>,<0|0|0|1>,<-0.8501|-3.4946|-5.416|-3.78>>;
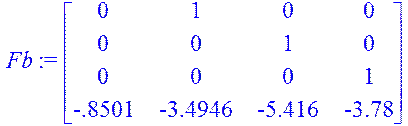
Нехай φ(λ) - аналітична функція. Тоді вона може
бути подана у вигляді степеневого ряду 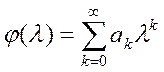 . Визначимо значення функції φ для
матричного аргументу А як матрицю φ(Α),
що обчислюється за формулою
. Визначимо значення функції φ для
матричного аргументу А як матрицю φ(Α),
що обчислюється за формулою 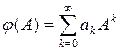 . φ(Α)=
. φ(Α)=![]() =
=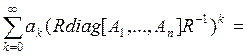
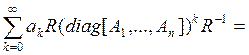
=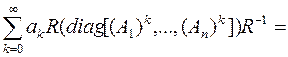 Rdiag(φ(A1)
),…, φ(An))R-1 .
Rdiag(φ(A1)
),…, φ(An))R-1 .
Отже, маємо загальну формулу обчислення функції від матриці, якщо всі власні значення – дійсні і різні то матриця Жордана має вигляд діагональної матриці, у якой на діагоналі стоять власні значення матриці А:
> J:=<<-1.226105292|0|0|0>,<0|-.9195803724-.3528703358*I|0|0>,<0|0|-.9195803724+.3528703358*I|0>,<0|0|0|-.7147339633>>;
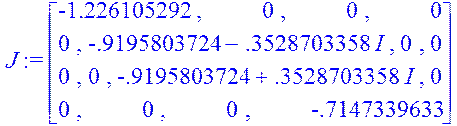
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.