Регулярные функции. Дифференцируемые функции. Условия Коши — Римана. Геометрический смысл производной, страница 9

§ 8, ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ           69

дит в луч arg w = 2л + 26, расположенный выше верхнего берега разреза. Аналогично, луч arg z = 2л — б переходит в луч arg w = = 4л — 26, примыкающий к нижнему берегу разреза.

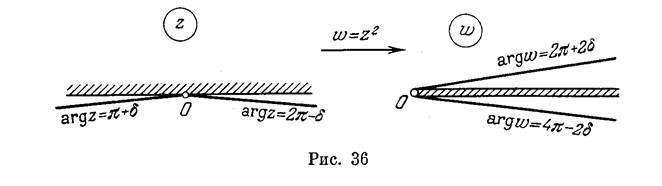
Отметим еще, что при отображении w = z правая полупло­скость (Rez>0) и левая полуплоскость (Rez<0) переходят в плоскость с разрезом по отрицательной действительной полуоси (рис.37). Q

Пример 4. Рассмотрим отображение

w = е\                         (8)

Найдем условие, которому должна удовлетворять область D, что­бы отображение (8) было однолистным в этой области. Если e^i^e^, т. е. е^~^= 1, то я     __<^ .(п. 6, § 4)                     |        ^^

Zi - Za = 2/cni            ^ 0  ^\z)           \        _

^                  \     ^<ш) (A=0, ±1.±2. ...). (9) |                  \     -"

Следовательно, для однолист-                  ^^г////п///////л^ ности отображения. (8) необхо-                     i       О димо и достаточно, чтобы об-  ^                / ласть D не содержала никакой  ?               /^/ пары различных точек, удов- '^0         -^^ летворяющих   условию   (9).  ^    •——--'l"'' В частности, отображение w = к   (i) == e^г является однолистным в го­ризонтальной полосе а < Im z <             Рис» 37 <Ь, 0<b-a-^2n.

Рассмотрим полосу Di: 0<Imz<2n (рис. 38). При отобра­жении (8) прямая z=x+iC (С—фиксировано, 0<С'<2я;

—<х><х<+°°), параллельная действительной оси и лежащая в полосе Di, переходит в линию w = е""¹"'⁰ = е* • е¹⁰, т. е. в луч arg w = С. Будем двигать прямую z = х + 1C параллельно дей­ствительной оси, непрерывно увеличивая С от 0 до 2я. Тогда луч arg w = С, являющийся образом прямой г = х + iC, поворачиваясь против часовой стрелки, опишет всю плоскость w. При этом пря­мые z =х(—°° <х < °°) и г=х+г2л, образующие границу

70                     ГЛ. II. РЕГУЛЯРНЫЕ ФУНКЦИИ

полосы Di, отобразятся соответственно на лучи arg w = 0 и arg w = 2л.

Таким образом, функция w = е\ однолистная в полосе 0 < <'1т2<2л, отображает эту полосу на плоскость с разрезом по лучу [0, +оо) так, что нижний край полосы переходит в верх­ний берег разреза, а верхний край полосы — в нижний берег разреза.

Заметим, что при отображении (8) отрезок z = Ci + iy (Ci — фиксировано, 0^у^2я), лежащий в полосе Di и параллельный

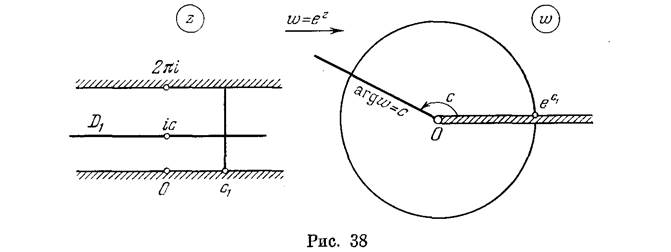
мнимой оси, переходит в «незамкнутую» окружность w == е⁰^¹⁹ (О ^ у ^ 2п) радиуса е i (точке Zi == Ci соответствует точка Wi = 6^е! верхнего берега разреза, а точке Zz == Ci + 2ni — точка

С   2Jli                                           ^                            ^\\

1Уд == е ^le , лежащая на нижнем берегу разреза и совпадающая геометрически с точкой Wi).

Аналогично можно показать, что полоса Dz: 2л<1тг<4я отобразится функцией w == e^z на плоскость с разрезом по лучу {О, +°°) так, что нижний край полосы Da перейдет в верхний берег разреза, а верхний край полосы — в нижний берег разреза. Точно так же можно установить, что функция w == е¹ однолистна в полосе Dh: 2(k— 1)л < Imz < 2/сл (/с—целое) и отображает эту полосу на плоскость w с разрезом по лучу [0, +оо). []

3. Понятие конформного отображения.

1. Сохранение угла между кривыми. Пусть функ­ция w==f(z) дифференцируема в некоторой окрестности точки Zo и пусть f'(zo)¥^:0. Рассмотрим гладкую кривую •у: z=o((), a=$fs£ji (рис. 39), проходящую через точку Zo=o(fo), ty^ e(a, ^). Обозначим 9 угол, образуемый касательной к кривой ^ в точке Zo и положительным направлением действительной оси (касательная считается направленной в ту же сторону, что и кривая). Тогда 6 == argo'((o).

Пусть ^'—образ кривой f при отображении w=f(z), т. е. f': w=w(_t}^:=f[a(t}}, cssSfsSp, а точка w„ — образ точки