Регулярные функции. Дифференцируемые функции. Условия Коши — Римана. Геометрический смысл производной, страница 7

Сравнивая (24) и (25), находим g' (х) = За;², откуда g(x)'=x^з+ + С, где С — действительная постоянная, и из (23) получаем v = —Зжу² + х³ + С. Искомая функция

/ (z) = и + iv = у³ - ^у + i {х³ - Зху²) + iC = i (z³ + С)

дифференцируема во всей комплексной плоскости. Q

4. Понятие регулярной функции. Введем одно из основных понятий теории функций комплексного переменного — понятие регулярной функции.

Определение 1. Пусть функция f(z) определена в окре­стности точки z== а (а^оо) и разлагается в ряд

/(z)= I c„(z-a)»,                    (26)

п==о

сходящийся в некоторой окрестности точки z = а (т. е. в круге |z—al<p, p>0). Тогда функция /(z) называется регулярной в точке z = а.

Функция /(z) называется регулярной в области D, если она регулярна в каждой точке области D.

64                     ГЛ. II. РЕГУЛЯРНЫЕ ФУНКЦИИ

Теорема 4. Если функция f(z) регулярна в точке z=a, то она дифференцируема в этой точке.

Доказательство. По условию, степенной ряд (26) схо­дится в некоторой окрестности точки а, откуда следует, что /(а)=Со. Рассмотрим отношение

-"й^^»^-)-.    ст

п=1

Так как ряд (27) равномерно сходится в круге |z—a|sSpi<p, то его сумма непрерывна в этом круге и в правой части (27) можно почленно перейти к пределу при z -> а (более подробно теория степенных рядов будет изложена в § 11), и этот предел равен d. Поэтому существует предел и левой части (27) при z ->- а, т. е. существует /^/ (а) = c^.

Замечание 1. В дальнейшем (§ 12) будет показано, что функция, дифференцируемая в области, регулярна в этой области.

00

Пример 6. Функция -,—— = ^, г" регулярна в точке z = О

i — Z    ^^и" п=0

(ряд сходится в круге |zl < 1). []

Определение 2. Пусть функция /(z) определена в окре­стности бесконечно удаленной точки и разлагается в ряд

00

/00=2^'                     (28)

П=0  ²

сходящийся в некоторой окрестности точки z == оо (т. е. в области Izl >R). Тогда функция /(z) называется регулярной в бесконеч­но удаленной точке.

Замечание 2. Из определения 2 следует, что функция /(г) регулярна в точке z = оо в том и только в том случае, когда функция g(^,)=f(Vt>) регулярна в точке S = 0. = 0. []

§ 8. Геометрический смысл производной

1. Понятие однолистности. В § 4 было введено понятие функ­ции комплексного переменного. Этому понятию можно дать сле­дующую геометрическую интерпретацию.

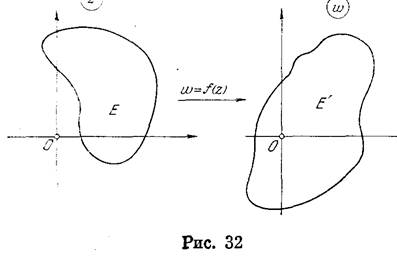
Пусть на множестве Е расширенной комплексной плоскости z определена функция w=f(z} и пусть Е'—множество ее зна­чений на плоскости w (рис. 32). Тогда говорят, что задано ото­бражение множества Е на множество Е''. Точка w^E' называ-