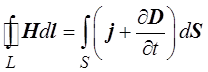Магнитомеханические явления. Электромагнитная индукция. Гармонические колебания. Затухающие колебания (Главы 4-7 учебного пособия по общей физике), страница 9

.

Читается это уравнение так: циркуляция вектора Н по любому замкнутому контуру равна полному току через поверхность, ограниченную этим контуром.

Уравнение показывает, что магнитное поле порождается как токами проводимости, так и изменяющимся электрическим полем.

5.7.  Уравнение Максвелла для циркуляции вектора Е

Как было показано в разд. 5.2, эдс электромагнитной индукции равна циркуляции вектора Е по контуру, пронизы-ваемому магнитным полем,  .

В свою очередь, в соответствии с законом Фарадея, эдс индукции равна производной от магнитного потока по времени (см. разд. 5.1)   .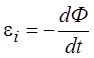

Учитывая, что магнитный поток по определению (см. разд. 3.8) равен 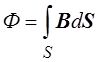, можем записать следующее соотношение:

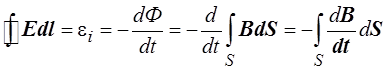
и окончательно

.

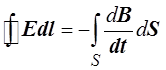Полученное уравнение и есть уравнение Максвелла для циркуляции вектора напряжённости электрического поля Е.

Данное уравнение Максвелла показывает, что изменяющееся магнитное поле порождает электрическое поле.

Уравнение Максвелла о циркуляции вектора Н и уравнение Максвелла о циркуляции вектора Е показывают, что переменные электрическое и магнитное поля неразрывно связаны между собой. Каждое из этих полей, изменяясь, порождает другое. Такая система связанных переменных электрического и магнитного полей называется электромагнитным полем (подробнее см.
разд. 10).

5.8.  Энергия магнитного поля

Рассмотрим изображённую на рисунке схему.

Переключение ключа из положения 1 в положение 2 вызывает отключение источника эдс от цепи. Опыт показывает, что это не вызывает мгновенного прекращения электрического тока.

Ток в цепи в этом режиме идёт за счёт эдс самоиндукции, возникающей в соле-ноиде.

Для поддержания тока в цепи необ-ходимо затрачивать энергию. Откуда она берётся?

Можно предположить, что ток в такой цепи существует за счёт энергии магнитного поля, созданного током, протекавшим в цепи.

Следовательно, магнитное поле должно обладать некоторой энергией.

Найдём величину энергии магнитного поля.

В контуре с индуктивностью L и током I

Ф = LI.

Изменение тока на dI означает изменение магнитного потока на dФ = LdI.

Ранее было установлено (см. разд. 3.9), что при изменении магнитного потока на dФ совершается работа dA = IdФ.

Следовательно, в данном случае должна быть совершена работа

dA = IdФ = LIdI.

Конечная работа, совершённая в рассматриваемом контуре при изменении тока от I_о до 0,

.

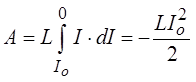Работа отрицательна, так как энергия контура уменьшается.

Энергия контура уменьшается до нуля, значит совершённая работа равна по величине начальному значению энергии магнит-ного поля:

Таким образом, энергия, запасённая в магнитном поле,

.

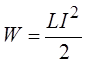Выражение для расчёта энергии магнитного поля можно записать и в иной форме:

.

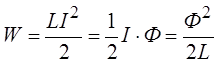Выражения для расчёта энергии, запасённой в магнитном поле, можно перевести и в другую форму. Сделать это можно следующим способом.

Как известно, для соленоида L = m_omn²V.

Тогда .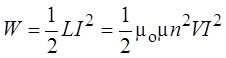

Поскольку для бесконечного соленоида В = m_omnI,

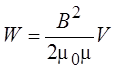
или

,

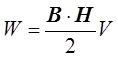где 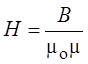 – напряжённость магнитного поля.

Обратите внимание: в полученное выражение входят только характеристики магнитного поля. Величины, характеризующие источник поля (например, соленоид), отсутствуют.

Это означает, что носителем энергии является само магнитное поле. Энергия, запасённая в магнитном поле, рассредоточена по всему пространству, занимаемому магнитным полем.

Если магнитное поле неоднородно, то величина 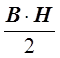 в разных точках различна.

В этом случае удобно использовать объёмную плотность энергии магнитного поля:

.

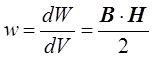(это энергия магнитного поля, запасённая в единице объёма).

Энергия, запасённая в конечном объёме неоднородного магнитного поля, может быть найдена следующим образом:

.

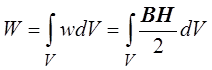Важно отметить, что последнее выражение позволит получить правильный результат только в линейных средах, или средах, в которых В и Н связаны линейно, т. е. когда магнитная прони-цаемость среды, в которой существует магнитное поле, не зависит от напряжённости магнитного поля (т. е. в пара- и диа-магнетиках).