В правой части равенства присутствует модуль вектора электрического смещения, который является характеристикой электрического поля в диэлектрике. Следовательно, правая часть равенства относится к той части цепи, где отсутствуют свободные носители заряда и где токи проводимости протекать не могут.
Тем не менее 
имеет размерность плотности тока.
Поэтому Максвелл предположил, что в диэлектрике может существовать особый ток, природа которого существенно отлич-на от природы тока проводимости. Он назвал этот ток током смещения.
По определению, плотность тока смещения
.
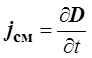Как отмечено выше,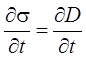 
, поэтому
jпр = jсм,
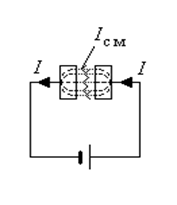т. е. плотности тока проводимости и
тока смещения в замкнутой цепи всегда равны. Таким образом, ток непрерывен не
только в цепях, состоящих из проводников, но и в цепях, содержащих непроводящие
элементы (например, конденсаторы).
Рассмотрим природу тока смещения.
Производная, расположенная в правой части равенства, может быть записана следующим образом:
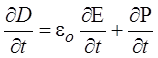
(здесь использовано определение вектора электрического смещения, данное в разд. 1.17).
Следовательно, jсм =
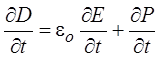, или в векторной форме
.
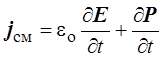Рассмотрим этот ток подробнее.
Слагаемое 
(производная от поляризованности по
време-ни) связано с процессами, протекающими в ходе поляризации диэлектрика.
Как отмечено в разд. 1.15, в полярных диэлектриках происходит поворот атомов так, чтобы их дипольный момент стал параллелен силовым линиям электрического поля.
В неполярных диэлектриках происходит смещение* элект-ронных оболочек атомов в одну сторону, а ядер – в противо-положную.
_____________________________
* Отсюда и происходит название тока смещения.
Поэтому можно сказать, что является плотностью тока, возникающего
из-за упорядоченного движения атомов диэлектрика в процессе его поляризации.
Слагаемое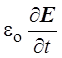 
не равно нулю, если с течением времени
изменяется напряжённость электрического поля.
Но электрическое поле может изменяться и там, где нет носителей заряда (например, в вакууме).
Следовательно, эта компонента тока смещения не связана с какими-либо зарядами. Она порождается изменяющимся электри-ческим полем.
Ток проводимости в проводниках создаёт магнитное поле.
Но тогда и ток смещения должен создавать такое же магнитное поле (так как jпр = jсм).
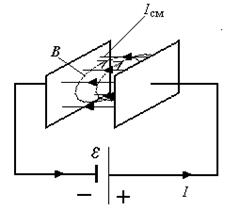
Экспериментальная проверка показала, что это предполо-жение верно. Между обкладками конденсатора существует точнотакое же магнитное поле, как и вокруг проводников, соединённых с обкладками.
Так была подтверждена правильность гипотезы Максвелла о существовании тока смещения и доказано, что токи смещения наряду с токами проводимости являются источником магнит-ного поля.
Ещё раз обратите
внимание на очень важную деталь: ток смеще-ния может существовать в среде,
не содержащей заряженных час-тиц (в вакууме). Если в такой среде имеется
изменяющееся во времени электрическое поле, то в ней суще-ствует и ток
смещения.
Кроме тока смещения, Максвелл ввёл понятие полного тока. Полный ток – это ток, равный сумме тока проводимости и тока смещения.
Плотность полного тока
.
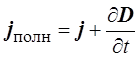В свою очередь, сила полного тока равна
.
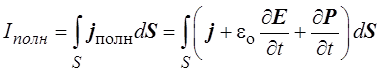Как показано в разд. 3.11, циркуляция вектора магнитной индукции равна произведению магнитной постоянной на алгебраическую сумму токов, охваченных контуром,
.
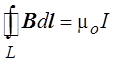По определению напряжённости магнитного поля
B = moH
(выражение записано для магнитного поля в вакууме).
Заменив вектор магнитной индукции на вектор напря-жённости получим выражение для циркуляции вектора Н:
.
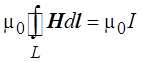Сократив mо и учитывая не только токи проводимости, но и ток смещения, получаем
.
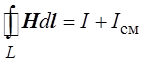Сила тока равна потоку вектора плотности тока (см. разд. 1.19):
.
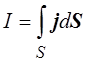С учётом последнего и принимая во внимание то, что плотность тока смещения равна производной от вектора электрического смещения по времени, получаем окончательное выражение для циркуляции вектора напряжённости магнитного поля
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.