Причиной возникновения эдс является сила Лоренца, действующая на свободные заряды в элементах контура, движущихся в магнитном поле.
Несколько иная картина в том случае, когда эдс возникает в неподвижном контуре, находящемся в изменяющемся магнитном поле. Здесь уже сила Лоренца не действует – проводник не перемещается в магнитном поле. Поэтому и причина возник-новения эдс здесь другая.
Анализируя эту ситуацию, Максвелл предположил (а впос-ледствии была установлена правильность гипотезы), что любое изменяющееся магнитное поле вызывает появление элект-рического поля.
Таким образом, в контуре, находящемся в изменяющемся магнитном поле, индуцируется электрическое поле, которое и вызывает появление электрического тока. Эдс индукции и в этом случае
.
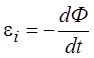Индукционное электрическое поле обладает существенными особенностями.
Во-первых, сейчас нельзя выделить часть контура, в которой локализован источник эдс. Электрическое поле порождается во всех элементах контура. Поэтому интеграл от Edlследует брать по замкнутому контуру:
.
Во-вторых, поскольку эдс отлична от нуля,
.
Это означает, что
индукционное электрическое поле отлично от электростатического, в котором 
(см. разд. 1.9).
В-третьих, поскольку , постольку силовые линии этого электрического
поля замкнутые. Такое электрическое поле называют вихревым.
Именно это поле вызывает появление электрического тока в неподвижном проводнике.
Любой контур с электрическим током порождает магнитное поле.
Если ток в контуре изменяется во времени, созданное им магнитное поле тоже будет изменяющимся.
В любом контуре,
находящемся в переменном магнитном поле, возникает эдс индукции .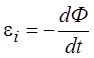
Отсюда следует, что в контуре с изменяющимся электри-ческим током должна возникать эдс, индуцированная магнит-ным полем, которое создано этим же контуром.
Поскольку эту эдс порождает сам контур, её называют эдс самоиндукции. Явление возникновения эдс самоиндукции называют явлением самоиндукции.
Определим величину эдс самоиндукции.
Магнитный поток Ф, охваченный контуром с током I, естественно, зависит от силы тока I, поскольку этот ток I и создал магнитный поток Ф.
Величина магнитного потока Ф прямо пропорциональна току I
Ф = LI,
где L – индуктивность контура.
Магнитный поток, порождённый контуром с током I, зависит от ряда факторов: во-первых, – от силы тока I; во-вторых – от формы контура (поскольку величины B и S связаны с формой контура); в-третьих, – от среды, в которой находится контур, т. е. от магнитной проницаемости среды m.
Это означает, что индуктивность контура L зависит от двух факторов – от формы контура и от магнитной проницаемости среды, окружающей контур.
Если форма и магнитная проницаемость не изменяются, индуктивность контура постоянна.
На основе закона Фарадея для эдс самоиндукции мы можем записать
.
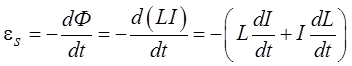Знак « – » в этом выражении показывает, что направление тока самоиндукции в контуре подчиняется правилу Ленца: если ток в контуре уменьшается, то ток самоиндукции направлен в ту же сторону (т. е. препятствует уменьшению тока), если же ток в контуре растёт, ток самоиндукции направлен против него.
Второй член в этом
выражении (
) отличен от нуля тогда, когда L зависит
от времени. Такая зависимость имеет место в двух случаях: когда с течением
времени изменяется форма контура; когда вблизи контура имеются ферромагнетики,
у которых m зависит от Н,
а в изменяющихся магнитных полях это означает зависимость m от времени.
Если же форма контура неизменна и m не зависит от Н, то
.
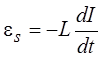Пример вычисления индуктивности приведён в разд. 3.12.
|
|
Рассмотрим два близко расположен-ных контура.
Ток I1, текущий в первом контуре, создаёт магнитное поле, пронизывающее и второй контур.
Магнитный поток через второй контур пропорционален создавшему его току
.
Если ток I1 изменится, то во втором контуре возникнет эдс индукции
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
