Магнитомеханические явления. Электромагнитная индукция. Гармонические колебания. Затухающие колебания (Главы 4-7 учебного пособия по общей физике), страница 13

Со стороны пружины на маятник действует упругая сила F =-kx (здесь х – смещение груза от положения равновесия; если начало координат совместить с положением равновесия груза, то х – координата груза).

На основании второго закона Ньютона и закона Гука

или

.

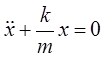Введём обозначение .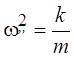

Теперь уравнение примет вид

.

Но это уравнение гармонического осциллятора. Следова-тельно, пружинный маятник является гармоническим осцил-лятором, и если пружина идеальна, отсутствует трение и нет других потерь энергии, то пружинный маятник, выведенный из положения равновесия, совершает гармонические колебания.

Величина  равна цикли-ческой частоте пружинного маятника. Из этого выражения видно, что частота колебаний маятника растёт с увеличением упругости пружины и умень-шением массы груза, подвешенного к ней.

Величина  – это скорость колеблющегося груза, а  – его ускорение в данный момент времени.

Отсюда видно, что для пружинного маятника, совершающе-го гармонические колебания, координата груза, его скорость и ускорение изменяются по гармо-ническому закону, т. е. соверша-ют гармонические колебания.

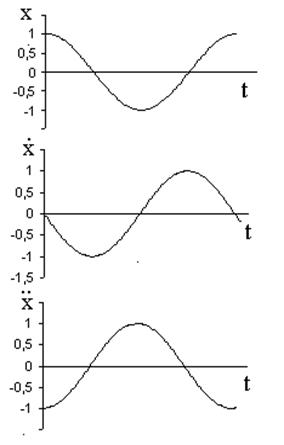
Из уравнений также видно, что начальные фазы колебаний сме-щения, скорости и ускорения гру-за различны. Это хорошо видно и на графиках (см. рисунок).

Обратите внимание: в тот мо-мент, когда смещение от положе-ния равновесия максимально, ско-рость груза равна нулю, а уско-рение максимально по величине и направлено против смещения (так как проекция смещения положи-тельна, а ускорения – отрица-тельна).

Период колебаний пружинного маятника .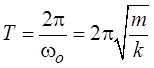

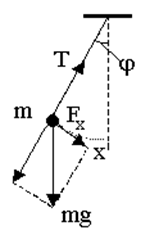6.4.2. Математический маятник

Рассмотрим материальную точку массой m, закреплённую на невесомой нерастяжимой нити длиной l.

Отклоним маятник от положения равно-весия на малый угол j.

Разложим силу тяжести mg, действующую на груз, на параллельную и перпендикулярную нити составляющие.

Составляющая, параллельная нити, ком-пенсируется силой натяжения нити Т, поэтому они не влияют на движение маятника. Следо-вательно, движение маятника определяется составляющей F_x, которая равна F_x = -mgsinj (минус в правой части обусловлен тем, что составляющая F_x всегда направлена против отклонения маятника от положения равновесия).

При малых углах отклонения кривизной траектории груза можно пренебречь, поэтому sinj = j = , где х – смещение груза от положения равновесия (здесь учтено, что при малых углах
sinj = j). Поэтому .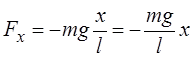

Введём обозначение 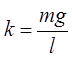. Тогда F_x = -kx. Это выражение похоже на закон Гука, определяющий величину силы, воз-никающей при упругой деформации тел. Следовательно составляющая F_x подобна упругой силе. Но, поскольку упругие деформации в рассматриваемой системе по условию отсутст-вуют, эту составляющую называют квазиупругой силой.

В соответствии со вторым законом Ньютона

;

;

.

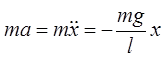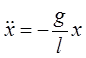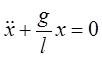Вводя обозначение 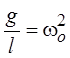, получаем

.

Таким образом, движение груза, закреплённого на нити, описывается дифференциальным уравнением гармонического осциллятора. Следовательно, математический маятник при малых углах отклонения совершает гармонические колебания. Они описываются уравнениями:

.

Период колебаний математического маятника .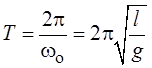

Период Т увеличивается с увеличением длины маятника и уменьшением ускорения свободного падения (кстати, на этом основаны практически применяющиеся способы измерения ускорения свободного падения).

Обратите внимание на то, что в выражение для расчета периода колебаний математического маятника не входит m. Следовательно, период колебаний математического маятника не зависит от массы груза.

6.4.3. Колебательный контур

Рассмотрим электрическую цепь, содержащую идеальный соленоид (это значит, что его сопротивление равно нулю) и конденсатор.

В соответствии со вторым правилом Кирхгофа, сумма разностей потенциалов на элементах контура равна сумме эдс, вклю-чённых в рассматриваемый контур.

В колебательном контуре эдс возникает в соленоиде. Это эдс самоиндукции e_L.