Магнитомеханические явления. Электромагнитная индукция. Гармонические колебания. Затухающие колебания (Главы 4-7 учебного пособия по общей физике), страница 11

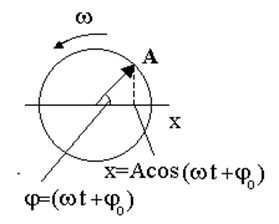
Выберем некоторую ось х и построим под углом j_о к оси х вектор, длина которого пропор-циональна амплитуде гармони-ческого колебания А.

Пусть этот вектор равномерно вращается против часовой стрел-ки с угловой скоростью, равной циклической частоте гармони-ческого колебания w. В этом слу-чае угол между вектором А и осью х в любой момент времени будет равен wt + j_о*.

Проекция вектора на ось х будет равна . Но это выражение описывает гармоническое колебание. Следо-вательно, проекция вектора А, вращающегося против часовой стрелки с угловой скоростью w, равной циклической частоте представляемого колебания, и будет гармоническим колебанием

______________________________

* В момент t= 0 угол равнялся j_о

. Начальная фаза представляемого гармони-ческого колебания равна углу j_о между вектором А в момент времени t = 0 и осью х, лежащей в плоскости вращения вектора.

6.3.  Сложение гармонических колебаний

6.3.1. Сложение одинаково направленных гармонических колебаний с равными частотами

Пусть некоторая точка участвует одновременно в двух гармонических колебаниях одного направления, имеющих рав-ные частоты.

Каким будет результирующий процесс?

Уравнения, описывающие эти колебания, имеют вид

.

Представим их в векторной форме (см. рисунок).

Сложив графически векторы А₁ и А₂, представляющие первое и второе колебание, получим результирующий вектор А.

Вектор А будет вращаться с той же угловой скоростью, что и складываемые векторы А₁ и А₂. Проекция вектора А на ось х будет изменяться с течением вре-мени по гармоническому закону. Следовательно, результирующий про-цесс представляет собой гармоничес-кое колебание, циклическая частота которого равна циклической частоте складываемых колебаний, амплитуда – А, а начальная фаза – j.

Для того чтобы найти значение А, выполним следующие действия:

.

Скалярно умножим вектор А сам на себя:

.

Учитывая, что скалярное произведение вектора на себя равно квадрату его модуля, получаем

и затем

Отсюда

.

Начальная фаза результирующего колебания, как это видно из рисунка, определяется соотношением

.

6.3.2. Сложение одинаково направленных колебаний с разными частотами. Биения

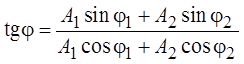Если частоты складываемых колебаний различны, то векторы А₁ и А₂ будут вращаться с разной скоростью, их взаимное расположение будет меняться. Поэтому с течением времени будут изменяться модуль результирующего вектора и скорость его вращения. Следовательно, амплитуда и циклическая частота результирующего колебания изменяются.

Таким образом, при сложении одинаково направленных гармонических колебаний разных частот возникают негармо-нические колебания.

Полученный вывод интересен ещё и тем, что позволяет увидеть следующее. Если результатом сложения гармонических колебаний разных частот является негармоническое колебание, то негармоническое колебание можно представить как сумму гармонических колебаний разных частот. Это возможно на самом деле и достаточно широко используется как в науке, так и в технике. Раздел физики, изучающий эту проблему, называется гармоническим анализом.

Определённый интерес представляет частный случай – сложение одинаково направленных колебаний с близкими частотами (т. е. w₁ » w₂).

Рассмотрим этот случай подробнее. Будем полагать, что начальные фазы и амплитуды складываемых колебаний одинаковы.

В этом случае уравнения, описывающие складываемые колебания имеют вид:

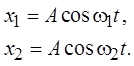
Результирующий процесс будет описываться выражением*

.

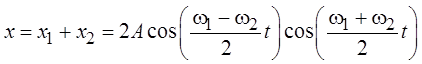Как видно из полученного выражения, результирующий процесс описывается произведением двух косинусов. Цикличес-кая частота первого косинуса очень мала (по условию w₁ » w₂), а второго приблизительно равна циклическим частотам склады-ваемых колебаний w₁ и w₂.

Это позволяет трактовать результирующий процесс как колебание с частотой, равной 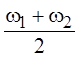, амплитуда которого медленно меняется по закону .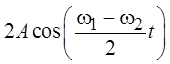

Такие колебания принято назы-вать биениями.