Магнитомеханические явления. Электромагнитная индукция. Гармонические колебания. Затухающие колебания (Главы 4-7 учебного пособия по общей физике), страница 16

,

Мы вновь получили однородное дифференциальное уравнение второго порядка.

Данное уравнение ничем не отличается от того, которое было получено для пружинного маятника в предыдущем разделе. Следовательно, его решение имеет такой же вид: , где .

Это означает, что в колебательном контуре с потерями энергии могут происходить затухающие колебания.

7.3.  Характеристики затухающих колебаний

Из решения дифференциального уравнения видно, что амплитуда затухающих колебаний уменьшается с течением времени по закону . Чем больше коэффициент b, тем быстрее уменьшается амплитуда колебаний. Поэтому его называют коэффициентом затухания.

Поскольку 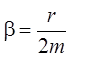, постольку колебания затухают тем быстрее, чем больше коэффициент трения r и чем меньше масса колеблющегося груза m.

Этот вывод достаточно легко понять – чем больше трение, которое препятствует всякому движению, тем быстрее пре-кратится колебательное движение реального осциллятора. Умень-шение массы означает, что уменьшается запас кинетической энергии осциллятора и поэтому при равном трении энергия будет быстрее израсходована на его преодоление.

Если обозначить символом t время, за которое амплитуда колебаний уменьшится в е раз, то , т. е. bt = 1 и .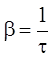

Таким образом, b есть величина, обратная времени, за которое амплитуда уменьшается в е раз.

Время t называют временем релаксации

В качестве характеристики затухания колебаний используется также логарифмический декремент затухания

,

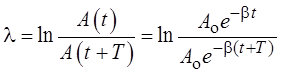где A(t) – амплитуда колебания в некоторый момент t; A(t + T) – амплитуда колебания через один период затухающего колебания.

Из последнего соотношения следует, что l = bT.

Целесообразность использования такой характеристики видна из следующего.

Поскольку l = bT, а b = 1/t, постольку 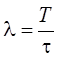. Но Т – это время, за которое совершается одно колебание, а t – время, за которое произойдёт, в общем случае, несколько колебаний*.

Тогда

,

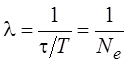где N_е – число колебаний, в ходе которых амплитуда уменьшится в е раз.

Таким образом, b и l являются характеристиками затухания, дополняющими друг друга: b показывает, как быстро затухают колебания, но при этом не содержит информации о количестве колебаний; l же показывает, за сколько колебаний амплитуда уменьшится в е раз, но ничего не говорит о времени, за которое произойдёт это уменьшение.

Из решения дифференциального уравнения также следует, что частота затухающих колебаний w меньше частоты колебаний идеального маятника w_о: .

Циклические частоты w и w_о соотносятся следующим образом. Допустим, маятник совершает затухающие колебания с частотой w; если избавиться от трения, он будет совершать гармонические колебания с частотой w_о.

Поскольку 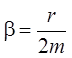, где r – коэффициент трения, с ростом трения частота затухающих колебаний уменьшается.

Колебания, совершаемые пружинным маятником с трением, не являются гармоническими.

____________________________

* В ходе этих колебаний амплитуда как раз и уменьшится в е раз.

Они также не являются и периодическими. Однако в физике принято использовать так называемый период затухающих колебаний 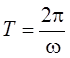; при этом под Т подразумевают время, за которое совершается одно колебание. 

7.4.  Критическое затухание

На качественной основе в разд. 7 было показано, что при достаточно большом трении колебания станут невозможны. Выведенная из положения равновесия колебательная система просто вернётся в него.

Такой режим в реальной колебательной системе наступит, если b возрастёт так, что выполнится условие , и  станет мнимой.

В этом случае решение диффе-ренциального уравнения принимает такой вид:

,

т. е. х от времени зависит экс-поненциально, колебаний нет. Система, которую вывели из положения равновесия, действительно постепенно возвращается в него (см. рисунок).

Затухание, при котором , называют критическим. При таком (и большем) затухании колебания в системе невозможны.