Явление гистерезиса заключается в том, что значение В при данном Н зависит от того, какое значение Н имела ранее. Например, если ферромагнетик не намагничен, то при Н = 0 В = 0.
Если ферромагнетик ранее
находился в магнитном поле с
Н > 0, то при Н = 0 В = Вост.
Если же ранее напряжённость
была отрицательной, то при
Н = 0 В =- Вост.
Ферромагнетики делят на две группы. Основанием для клас-сификации является коэрцитивная сила.
Коэрцитивная сила показывает, насколько трудно раз-магнитить ферромагнетик. Если коэрцитивная сила велика, то ферромагнетик размагнитить трудно. Такие ферромагнетики на-зывают магнитожёсткими. Из жёстких ферромагнетиков изго-тавливают постоянные магниты.
Если коэрцитивная сила мала, ферромагнетик можно размагнитить, почти не затрачивая на это энергию. Такие ферромагнетики называют магнитомягкими. Из них изготав-ливают сердечники трансформаторов.
Рассмотрим магнитное поле вблизи границы раздела двух сред с различной магнитной проницаемостью m1 и m2.
Допустим, что магнитное поле не перпендикулярно границе раздела двух сред.
Разложим векторы В и Н на две компоненты, из которых одна параллельна границе раздела двух сред, а вторая – перпендикулярна. Перпендикулярную компоненту назовём нормальной, а параллельную – тангенциальной.
Начнём с рассмотрения нормальной компоненты вектора магнитной индукции Вn. Воспользуемся для этого теоремой Гаусса для магнитного поля (см. разд. 8,8).
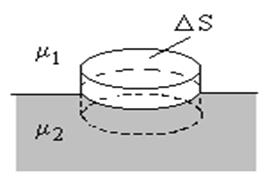Выделим
вблизи границы раздела двух сред цилиндрический объём бесконечно малой высоты с
площадью основания DS. Верхнее
основание расположено в среде с магнитной проницаем-остью m1, а нижнее – в
среде с m2.
Согласно теореме Гаусса, маг-нитный поток через замкнутую поверх-ность равен нулю.
В данном случае полный маг-нитный поток через выбранную поверхность равен сумме потоков Вn через верхнее и нижнее основания и через боковую поверхность цилиндра.
Поскольку высота боковой поверхности бесконечно мала, магнитный поток через неё бесконечно мал. Следовательно, полный магнитный поток равен сумме потоков через верхнее и нижнее основания.
Полный магнитный поток нормальной компоненты вектора магнитной индукции равен нулю, следовательно, потоки через верхнее и нижнее основания равны между собой
Bn1DS = Bn2DS.
Это означает, что нормальная компонента вектора магнитной индукции на границе раздела двух сред не изменяется
Bn1 = Bn2.
По определению напряжённости В = m0mН, поэтому
m1Нn1 = m2Нn2
и
.
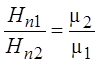Таким образом, нормальная компонента вектора напряжён-ности магнитного поля на границе раздела двух сред изменяется. Значение нормальной составляющей напряжённости магнитного поля в средах с разной магнитной проницаемостью различно.
Перейдём к
рассмотрению тангенциальной компоненты векторов В и Н.
Воспользуемся для этого теоремой о циркуляции вектора
напряжённости магнитного поля (см. разд. 4.2.).
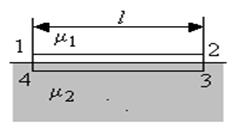
Выделим вблизи границы раздела двух сред замкнутый контур 1-2-3-4 прямоугольной формы (см. рисунок).
Длина горизонтальной стороны прямоугольника равна l, а высота прямоугольника бесконечно мала.
Если на границе раздела
двух сред нет тока, то 
, т. е. циркуляция вектора
напряжённости магнитного поля на границе раздела двух сред равна нулю.
Компоненты циркуляции по сторонам прямоугольника, перпендикулярным границе разделы пренебрежимо малы, так как высота прямоугольника бесконечно мала.
Компоненты циркуляции по параллельным
сторонам соответственно равны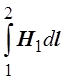 
и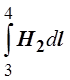 
.
Если длина участков 1-2 и 3-4 настолько мала, что напряжённости можно считать постоянными, то Н1 и Н2 можно вынести за знак интеграла. Тогда в результате интегрирования получим векторы l12 и l34, направление которых определяется направлением обхода контура.
Таким образом, циркуляция вектора напряжённости на границе раздела двух сред оказывается равной H1. l12 + H2. l34 = 0.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.