Программа определения места повреждения на воздушной линии электропередачи, страница 4

Линейные преобразования используются не только для описания разъёмов. Это и инструмент для представления результатов расчёта в удобной форме. Так, если расчёт фрагмента сети был выполнен в симметричных составляющих, то в выводной файл можно поместить значения в фазных координатах. Для этого сле­дует соответствующие узлы или многополюсники маскировать , наложив на них маску и сопоставив этой маске требуемое преобразование. Маску можно рассмат­ривать как разъём специального назначения: на его выходе величины оказыва­ются представленными в простой для восприятия форме.

Допустим, расчёт в части сети с изолированной нейтралью велся в 2-фазной системе прямой и обратной последовательностей. Тогда для получения токов фаз A, B и C в каком-либо полюсе следует наложить на этот полюс маску с матрицей M, приведенной в формуле 1.1.

Получить же напряжения фаз A, B и C для узла в этой части схемы, как го­ворилось ранее, принципиально невозможно: они определяются неоднозначно. Однако если принять допущение, что, скажем, нулевая составляющая напряжения должна быть равна нулю, то этого достаточно, чтобы можно было вычислить тройку напряжений U_m после маскировки. Дополнив уравнение  усло­вием равенства нулю суммы фазных напряжений, мы получим:

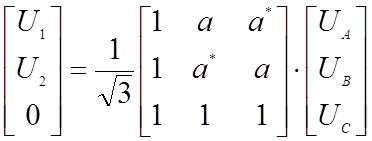
Отсюда можно получить, что , где M – всё та же матрица 1.1

Допущение о равенстве нулю напряжения нулевой последовательности можно и не принимать: напряжения можно отсчитывать не относительно гипотетической нейтральной точки, а от относительно одной из фаз, при этом следует указать иную матрицу преобразования.

Маска описывается точно так же, как и разъём, то есть в результате маски­ровки вектор токов умножается на матрицу преобразования:

.

Для напряжений же, согласно определению разъёма, должно иметь место соотношение:

,

т.е. для обсуждаемого примера сети с изолированной нейтралью:

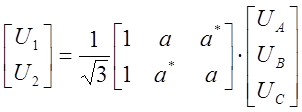
По маскированным напряжениям U_m фаз A, B, C можно было бы найти не­маскированные напряжения U прямой и обратной последовательностей. Но опре­делить маскированные напряжения по немаскированным нельзя.

В программе предлагается [8] следующий выход из этой ситуации: принять, что

,

где – это матрица, псевдообратная по отношению к M.

(1.2)

Если M имеет строк больше, чем столбцов, то

;   

если M имеет столбцов больше, чем строк, то

;

если M – квадратная матрица, то M⁺ совпадает с обратной;

для любых матриц

.

При определении U_m по формуле , будет гарантирована взаимная непротиворечивость прямого и обратного преобразований:

Нетрудно для матрицы M из 1.1 получить, что

,

и поэтому преобразования для токов и напряжений, задаваемых этой матрицей, совпадают!

Условие  справедливо и для перехода от полной системы симмет­ричных составляющих, включая и нулевую компоненту, к фазным. Поэтому при такого рода преобразовании (и, естественно, обратном) токи и напряжения преоб­разуются по единому закону описанному выше.

В общем случае это не так. Продемонстрируем, принцип получения мат­рицы преобразования для желаемой маски на примере. Допустим, мы захотели преобразовать напряжения прямой и обратной последовательностей в фазные ко­ординаты таким образом, чтобы эти напряжения отсчитывались не относительно нейтральной точки, а относительно фазы A. Закон обратного преобразования на­пряжений   пришлось бы дополнить условием U_A=0:

.

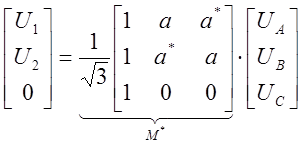Отсюда

.

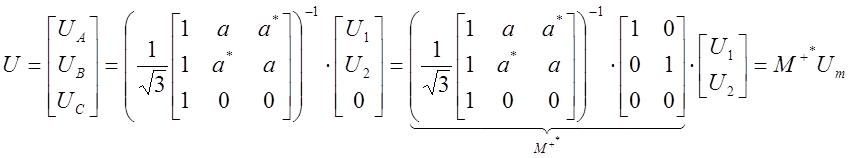Итак, матрица прямого преобразования напряжений M+* получена. Теперь по формуле (1.2) можно получить и матрицу прямого преобразования токов M, которую и нужно будет задавать в качестве исходных данных программе «Маска­рад».

1.3  Статус многополюсника

Для многополюсника любого типа должен быть указан его статус. Статус задается одним из четырёх возможных кодов:

"    " – новый многополюсник (его код – пробел);

"@" – старый;

"Y" – вне схемы;

"U" – нелинейный.

Новый многополюсник добавляется к расчётной схеме, его матрица Y вы­числяется и помещается в Y-файл.