Программа определения места повреждения на воздушной линии электропередачи, страница 3

Числа фаз с внешней и внутренней сторон разъёма могут быть разными. Например, если МП моделирует трансформатор с изолированной нейтралью и представлен схемой замещения в симметричных составляющих, то, поскольку для токов нулевой последовательности он обладает бесконечным сопротивлением, достаточно ограничиться схемами прямой и обратной последовательностей, т.е. фаз будет не 3, а 2. При этом внутренняя часть разъёма будет содержать 2 фазы: одна будет подключаться к подсхеме прямой последовательности, а другая – к схеме обратной последовательности. С внешней стороны разъём должен иметь 3 фазы: для подключения к фазам A, B и C узла. Внутри разъёма токи и напряжения должны преобразовываться из симметричных составляющих (прямая + обратная) в фазные. То есть токи и напряжения подвергаются  некоторому линейному пре­образованию, при котором сохраняется суммарная мощность фаз.

Исходная информация о режиме сети задается в узловой форме. Преду­смотрено 3 типа узлов: базисный (балансирующий), нагрузочный и генераторный. Генераторные узлы могут быть только 1-фазными. Нагрузка может быть много­фазной. Она подключается к узлу так же, как и полюс МП, т.е., возможно, через разъём.

Параметры некоторых элементов, например, узлов, 3-фазных 2-полюсников можно распечатывать и (или) задавать в симметричных составляющих. В про­грамме принят американский вариант преобразования Фортескью с очередностью последовательностей: прямая, обратная, нулевая (1-2-0):

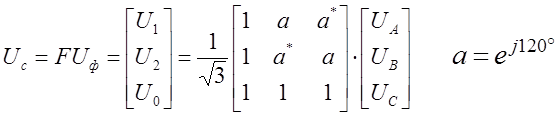
Множитель  сохраняет неизменной суммарную мощность всех трех фаз после преобразования:

(Звёздочкой обозначена операция эрмитова сопряжения).

Следует иметь в виду, что токи и напряжения прямой последовательности в симметричном режиме оказываются в  раз больше фазных.

Токи, протекая через разъём, подвергаются преобразованию. Точно так же и напряжения по разные стороны разъёма различны. Преобразование для токов и напряжений различны, но взаимосвязаны. Они задаются одной и той же матрицей M, в общем случае прямоугольной. Преобразование иллюстрируется на рисунке 1.3.

                                        

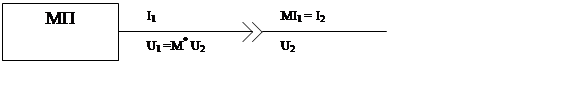
Рис. 1.3 Преобразование координат.

Если мы задаем закон преобразования для токов и напряжений, то тем са­мым мы задаем и закон преобразования мощностей. Так, суммарная мощность всех фаз после преобразования оказывается равной

.

Таким образом, оказывается, что суммарная мощность фаз преобразованию не подвергается. Благодаря этому сохраняются перетоки мощностей, а также не ме­няются потери активной и реактивной мощностей в каждом из МП.

Примером преобразования может служить переход от системы прямой и обратной последовательностей, обсуждавшийся выше, к фазным координатам.

(1.1)

   

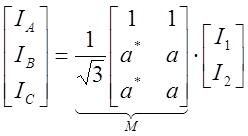
Для этого случая расчёт режима сводится к решению узлового уравнения, в результате определяются узловые напряжения. Напряжение же некоторого по­люса можно вычислить по соответствующему узловому напряжению лишь в том случае, если число фаз в полюсе не меньше числа фаз в узле (число столбцов в матрице преобразования не меньше числа строк). В данном примере это условие не соблюдается.

Важно иметь в виду, что невозможность расчёта напряжений полюса объясняется не недостатком программы «Маскарад», а природой вещей: уровень напряжения сети с изолированной нейтралью может быть принят любым: перетоки мощностей зависят лишь от разностей напряжений.

Заметим, если фрагмент с изолированной нейтралью представить не в двух-, а в трёхфазной системе координат, добавив к прямой и обратной еще нулевую по­следовательность, то матрица узловых проводимостей сети окажется вырожден­ной и расчёт режима произвести не удастся. Введение разъёмов-преобразователей это проблему снимает. Это является еще одним доводом в пользу их применения.