Программа определения места повреждения на воздушной линии электропередачи, страница 12

Многополюсники, моделирующие начальный и конечный участки ЛЭП, подключаются к месту повреждения вторыми полюсами. Фазы их первых полю­сов являются первыми фазами формируемой сборки. Схему подключения этих фаз в базе данных не храним, а формируем её программно. Чтобы присвоить по­следние номера фазам висячего полюса, увеличиваем сформированные их номера на общее число фаз первых полюсов начального и конечного многополюсника.

  j=0

Перебираем многополюсники, моделирующие начальный и конечный уча­стки ЛЭП и производим сквозную нумерацию первых их полюсов.

do m=1,2

     do p=F(1,m),T(1,m) 

      j=j+1

      Phase(p)=j

    end do

  end do

  Формируем массив соединения фаз вторых полюсов начального и конеч­ного многополюсника

  do i=1,kfm/2

                 MPsMP(i)=i

  enddo

Фазы второго полюса первого многополюсника подключаются к фазе вися­чего или земляного полюса поврежденного многополюсника

  Phase(F(2,1):T(2,1))= MPsMP

Фазы второго полюса второго многополюсника подключаются к фазе вися­чего или земляного полюса поврежденного многополюсника

  Phase(F(2,2):T(2,2))= MPsMP

Фазы  первого и второго полюса  многополюсника – вредителя подключа­ются к фазе висячего или земляного полюса поврежденного многополюсника.

  Phase(F(1,3):T(2,3))= kz

 Присваиваем последние номера фазам висячего полюса, для чего увеличи­ваем сформированные их номера на общее число фаз первых полюсов начального и конечного многополюсника.

  Phase(F(2,1):T(2,1)) = Phase(F(2,1):T(2,1)) + j

  Phase(F(2,2):T(2,2)) = Phase(F(2,2):T(2,2)) + j

  Phase(F(1,3):T(2,3)) = Phase(F(1,3):T(2,3)) + j

Определяем  размерность матрицы Y до исключения висячего полюса

  NPh = MaxVal(Phase)

  if (NPh > NPhMP) then

    write (Msg,'(a,i3,1h.)') &

      'Общее число фаз в смежных с повреждением многополюсниках превы­сило',NPhMP

    call AbortDlg(Msg)

    ier=10; goto 99

  end if

 Обнуляем формируемую матрицу Y

Y(:NPh*NPh)=0

2.2.4 Формирование матрицы Y поврежденного многополюсника и      исключение из нее висячих и земляных полюсов

Формируем матрицу Y поврежденного многополюсника  для чего обраща­емся к процедуре коррекции матрицы узловых проводимостей сборки при под­ключении к ней еще одного многополюсника.

  call AddYMP (Y1Ptr,Sum(NPhP(:,1)),Y,NPh,Phase(F(1,1)))

  call AddYMP (Y2Ptr,Sum(NPhP(:,2)),Y,NPh,Phase(F(1,2)))

  call AddYMP (YFPtr,Sum(NPhP(:,3)),Y,NPh,Phase(F(1,3)))

Произведём исключение висячих фаз серией шагов Жордана.

Суть этого преобразования рассмотрим на примере матричного уравнения, записанного с помощью матрицы узловых проводимостей в блочной форме:

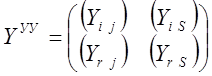
На основе этой матрицы запишем систему узловых уравнений:

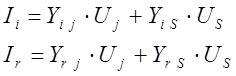
Решим уравнение с номером r относительно напряжения Us и подставим полу­ченное значение во все остальные уравнения.

Строка r и столбец s, используемые для определения напряжения Us, назы­ваются главными строками и столбцами, а элемент Yrs – главным элементом в процессе преобразования исходной матрицы Y^УУ. В результате преобразования получим матрицу:

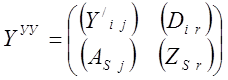
Элементы которой вычисляются следующим образом:

-  место главного элемента занимает его обратная величина  по­этому этот элемент не должен быть вырожденным;

-  прочие элементы главного столбца умножаются справа на обратную ве­личину главного элемента:  

-  прочие элементы главной строки умножаются слева на обратную вели­чину главного элемента и меняют свой знак на противоположный: ;

-  прочие элементы, не принадлежащие ни главному столбцу, ни главной строке, вычисляются по формуле:  .

Выполненный шаг исключения Жордана, по существу, означает перемену мест между напряжениями Us и током Ir, то есть напряжение Us из числа незави­симых переведен в ранг зависимых величин, а ток Ir наоборот, из зависимой ве­личины превратится в независимую.

O = HOPMA1(Y,NPh)*.0001 - Минимально допустимое значение опорного элемента

  do j=NPh, Sum(NPhP(1,1:2))+1,-1

   делаем шаг Жордана

   call JordK (Y,NPh,NPh,j,j,O,ier)

    if (ier/=0) then