Расчет и проектирование рельсовой колеи. Расчет и проектирование обыкновенного одиночного стрелочного перевода, страница 9

2.3 Определение основных параметров эпюры стрелочного перевода

2.3.1  Теоретическая длина стрелочного перевода

Теоретической длиной называется расстояние от начала остряков до математического центра крестовины.

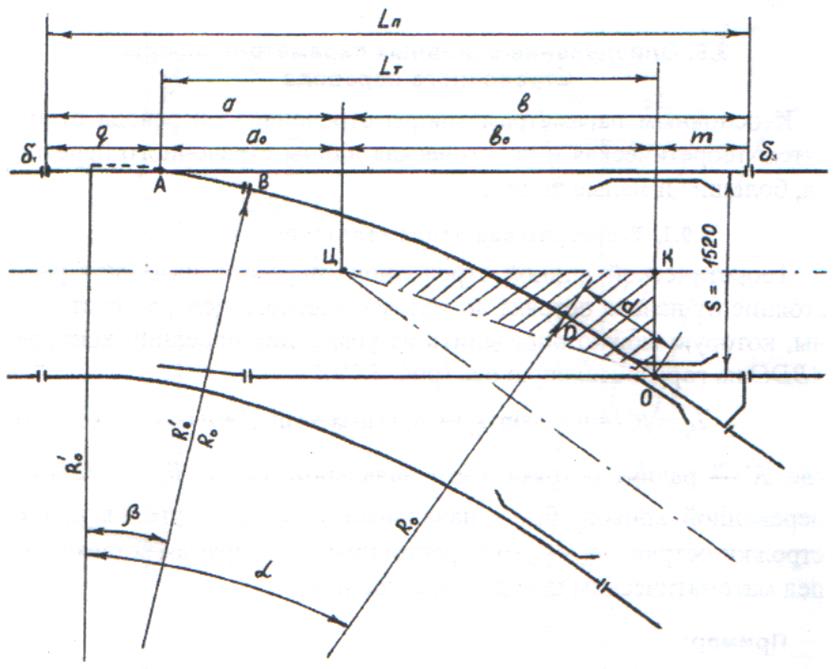
Рисунок 2.7 – Основные геометрические размеры стрелочного перевода

Эту длину найдем по формуле (2.41).

                      (2.41)

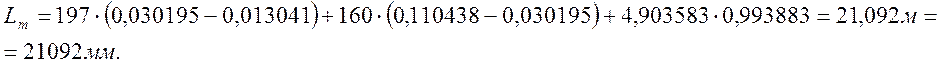
Принимаем теоретическую длину крестовины L_т=21092 мм.

2.3.2  Практическая длина стрелочного перевода

Практической длиной называется расстояние от оси зазора в переднем стыке рамного рельса до оси зазора в заднем стыке крестовины.

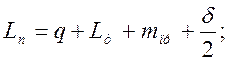                                               (2.42)

где: δ – величина стыкового зазора, δ=8 мм;

       q – величина переднего вылета рамного рельса;

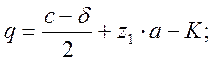                                                  (2.43)

где: a – величина пролёта, а=500 мм;

        с – стыковой пролёт, с=420 мм;

        δ – стыковой зазор, δ=8 мм;

        z₁ – число пролетов между осями переводных брусьев в зоне переднего вылета рамного рельса, z₁=5 шт.;

        К – смещение начала остряка относительно оси первого бруса, К=41 мм.

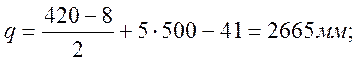
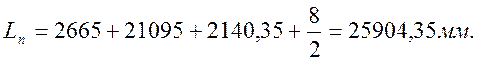
Окончательно принимаем практическую длину стрелочного перевода L_п=25904,35 мм.

2.3.3  Малые и большие полуоси стрелочного перевода

Расстояние от центра стрелочного перевода до математического центра крестовины b₀ (см. рис. 2.7) определяем  из прямоугольного треугольника ЦКО:

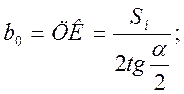                                             (2.44)

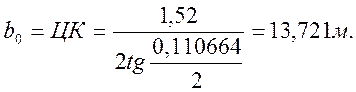
Расстояние от центра перевода до начала остряка:

                                                 (2.45)

Расстояние от центра стрелочного перевода до оси зазора переднего стыка рамного рельса:

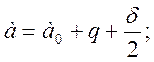                                               (2.46)

где: q – передний вылет рамного рельса, q=2,665м.

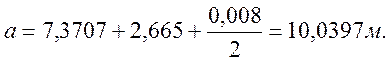
Расстояние от центра стрелочного перевода до оси зазора в хвосте крестовины:

                                                  (2.47)

где: m – длина хвостовой части крестовины, m=3,514м.

2.4  Длина остряка. Полный стрелочный угол и ордината в корне остряка

Длину остряка определяют из условий обеспечения требуемой величины желоба между рамным рельсом и остряком при переводе стрелки на прямой путь с шагом Ш.

Угол поворота остряка:

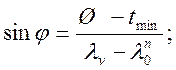                                              (2.48)

где: Ш – шаг остряка, Ш=147мм;

        - длина зоны примыкания остряка к боковой грани рамного рельса = 3377мм;

         - расстояние от острия оси I переводной кривой, измеряемое в долях рельса, =360мм;

         t_min – величина желоба, t_min=67мм.

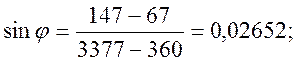
Длина остряка:

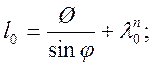                                                  (2.49)

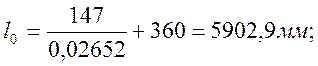
Полный стрелочный угол:

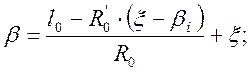                                         (2.50)

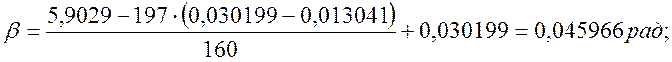
Проекция остряка на рамный рельс:

                            (2.51)

Ордината в корне остряка:

                                   (2.52)

Размер желоба между остряком и рамным рельсом:

                                                   (2.53)

2.5   Длина рамных рельсов

Рамными называются рельсы, которые служат основой стрелки и отличаются от стандартных наличием крепежных отверстий, а также подстрожкой боковой грани головки рельса для укрытия остряка от ударов подрезанных гребней колёс подвижного состава.

Длина рамного рельса:

                                              (2.54)

где:  q – передний вылет рамного рельса;

          - проекция криволинейного остряка на прямое направление рамного рельса;

         g – задний вылет рамного рельса.

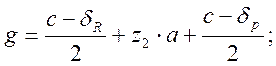                                          (2.54)

где: с – расстояние между осями стыковых брусьев, с=420мм;

        δ_R – расчётный стыковой зазор в корне остряка, δ_R =5мм;

        δ_р – стыковой зазор на заднем винте, δ_р=8мм;

        z₂ – число пролетов в пределах заднего вылета рамного рельса, z₂=2;

        a – величина пролёта, а=500 мм.

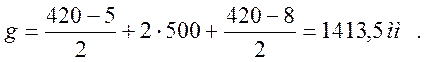
Тогда определим длину рамного рельса:

2.6        Ординаты для разбивки стрелочного перевода

Ординаты для разбивки стрелочного перевода определим в табличной форме. Для начала найдем конечную абсциссу:

                                           (2.55)

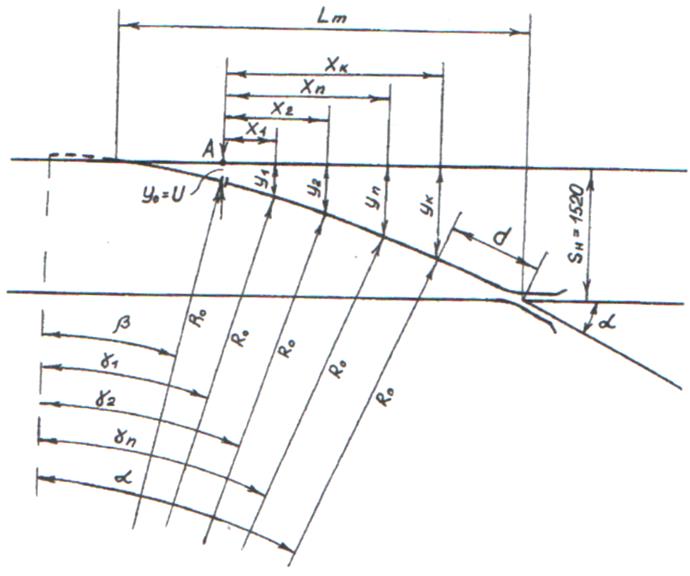
Рисунок 2.8 – Схема к определению ординат переводной кривой.