-
полная длина кривой ![]() =681,782м.
=681,782м.
Также был рассчитан порядок укладки укороченных рельсов в количестве 16 штук по внутренней нити кривой.
2 Расчёт и проектирование одиночного обыкновенного стрелочного перевода
Стрелочный перевод состоит из стрелочной части, крестовинной части и путей между ними.
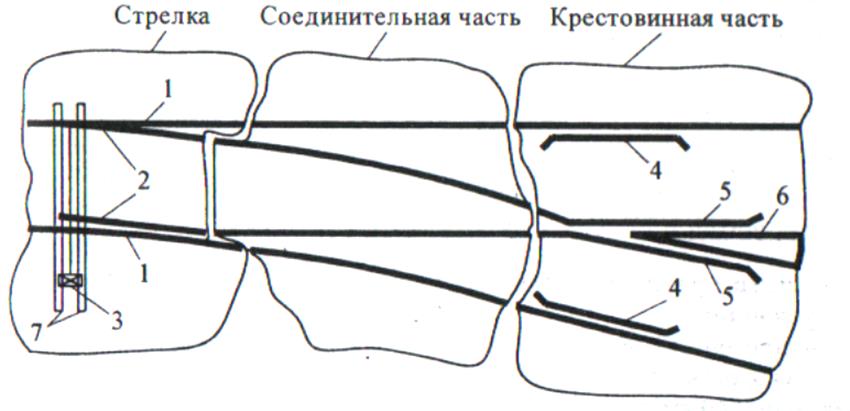
Рисунок 2.1 – Одиночный обыкновенный стрелочный перевод (основные части)
1 – рамные рельсы; 2 – остряки; 3 – переводной механизм; 4 – контррельсы;
5 – усовики; 6 – сердечник; 7 – переводные брусья.
2.1 Основные параметры стрелки
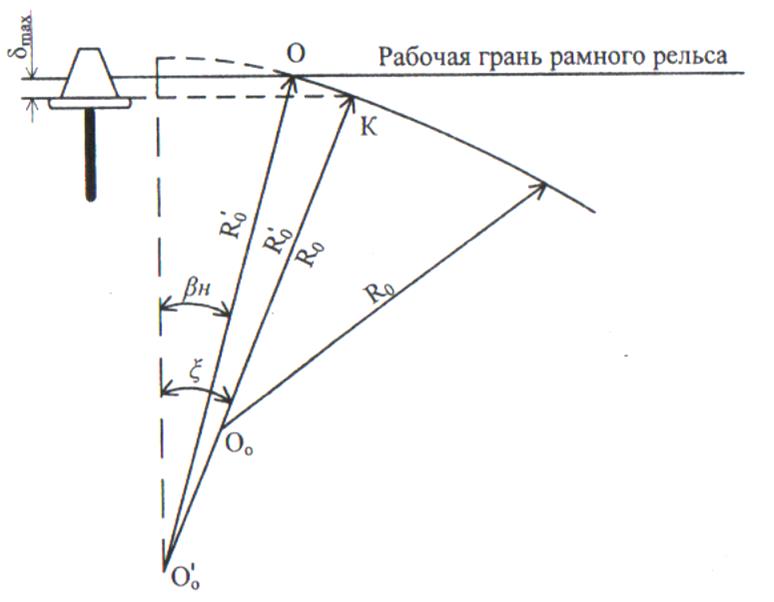
Рисунок 2.2 – Расчётная схема определения основных параметров стрелки.
К основным параметрам стрелки относятся:
1)
![]() -
радиус начальной части остряка в зоне возможных ударов гребней
-
радиус начальной части остряка в зоне возможных ударов гребней
колёс, м;
2)
![]() -
радиус остальной части остряка и переводной кривой, м;
-
радиус остальной части остряка и переводной кривой, м;
3) βу – угол удара гребней колёс, рад;
4) βн – начальный угол остряка бокового направления, рад;
5) λv – длина зоны примыкания остряка к боковой грани рамного рельса, м;
6) ξ – центральный угол, рад.
Радиус кривизны начальной части остряка, где центробежное ускорение возникает
внезапно, определяется из выражения
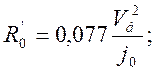 (2.1)
(2.1)
а радиус остальной части остряка и переводной кривой
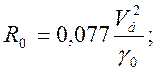 (2.2)
(2.2)
где: Vб – скорость движения на боковой путь, Vб=35 км/ч;
j0 – допустимая величина внезапно появляющегося центробежного ускорения, j0=0,48 м/с2;
γ0 – допустимое значение непогашенного ускорения, γ0=0,59 м/с2.
Рассчитаем значения ![]() и
и ![]() по
формулам (2.1) и (2.2)
по
формулам (2.1) и (2.2)
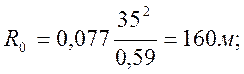
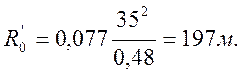
При входе экипажа в стрелочный перевод происходит удар гребней колёс в остряк бокового пути под углом βу.
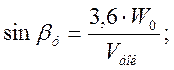 (2.3)
(2.3)
где: W0 – величина, пропорциональная потере кинетической энергии при ударе в остряк, W0=0,225 м/с.
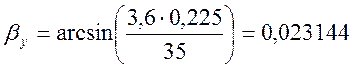 рад.
рад.
Начальный угол остряка определим из зависимости между
максимально вероятным зазором, с которым колесо подходит к остряку βн,
углом удара βу и радиусом ![]() .
.
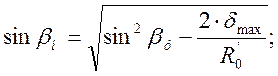 (2.4)
(2.4)
где: δmax – максимальный вероятный зазор между гребнем колеса и рамным рельсом, δmax=0,036 м.
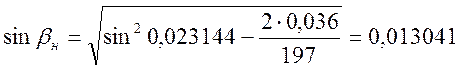 ;
;
cosβн=0,999914;
βн=0,013041 рад.
Расчёт длины строжки λv и угла ξ ведется в следующем порядке:
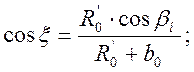 (2.5)
(2.5)
где: b0 – ширина головки остряка на расчётном уровне, b0=72,8·10-3м.
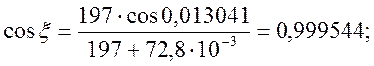
![]() рад.
рад.
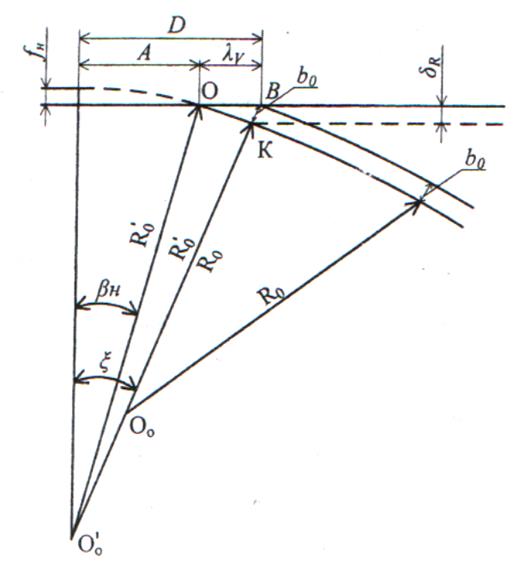
Рисунок 2.3 – Схема к определению длины примыкания остряка к рамному рельсу
Согласно рисунку 2.3:
![]() (2.6)
(2.6)
где:
![]() (2.7)
(2.7)
![]()
![]() (2.8)
(2.8)
![]()
![]()
Определим
ординату точки изменения радиуса ![]() на
на ![]() - δR:
- δR:
![]() (2.9)
(2.9)
![]()
2.2 Основные параметры крестовины
К основным параметрам крестовины относятся:
- угол крестовины α;
- марка крестовины 1/N = tg α;
- передний вылет крестовины n;
- задний вылет крестовины m.
2.2.1 Угол крестовины и её марка
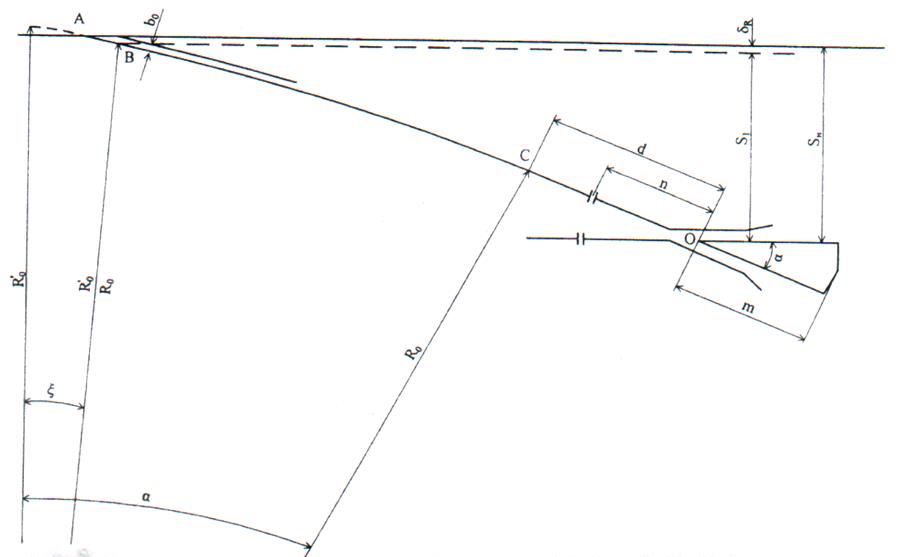
Рисунок 2.4 – Схема к определению марки крестовины
Угол крестовины определим по уравнениям:
![]() (2.10)
(2.10)
где: Sн – нормативная ширина колеи, Sн=1520мм;
d – величина прямой вставки перед крестовиной.
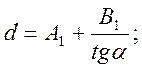 (2.11)
(2.11)
![]() (2.12)
(2.12)
где: p – размер прямой вставки между концом переводной кривой и передним стыком крестовины, р=1000мм;
![]() =316мм для цельнолитой крестовины рельсов Р
65;
=316мм для цельнолитой крестовины рельсов Р
65;
В1 = 283мм для цельнолитой крестовины.
![]()
![]() (2.13)
(2.13)
S1=1520-72,890=1447,11мм.
Сделав преобразования, получим:
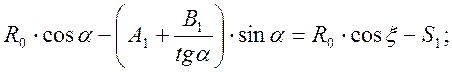 (2.14)
(2.14)
Обозначим правую часть равенства (2.14) через С, т.е.
![]() (2.15)
(2.15)
![]()
Тогда:
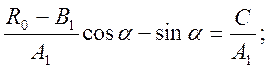
![]() (2.16)
(2.16)
Примем:
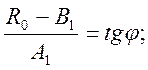 (2.17)
(2.17)
Найдем угол φ из выражения (2.17):
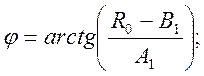 (2.18)
(2.18)
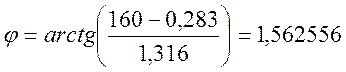 рад;
рад;
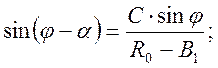 (2.19)
(2.19)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.