Теоретические основы параметрических методов обработки экспериментальных данных (Раздел 2 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 7

Пусть случайная величина  имеет плотность распределения , а результаты наблюдения над величиной  представляют собой простую (повторную) случайную выборку

                                             .

Вероятность появления конкретной реализации X_<n> пропорциональна элементу вероятности распределения случайного вектора :

.                                                             

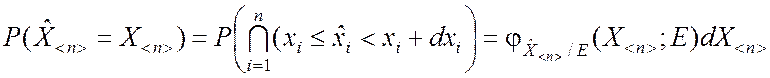(2.3.2)

Плотность распределения для простой выборки представляется выражением

                     . 

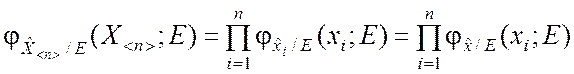Функция оцениваемого состояния  E  вида

                                             (2.3.3)

называется функций правдоподобия.

Принцип максимального правдоподобия состоит в утверждении, что при данной реализации X_<n> вектора  наиболее правдоподобным, т.е. наиболее близким к действительному состоянию, является то значение  оценки состояния исследуемого объекта, при котором вероятность (2.3.2), а следовательно, и функция правдоподобия (2.3.3) максимальны.

Исходя из данного утверждения, для определения наиболее правдоподобного значения состояния E необходимо найти такое значение , которое обеспечивает экстремум функции правдоподобия. Если оценивается несколько параметров  E₁,  E₂,…,E_k  какого-либо состояния, то решение данной задачи сводится к нахождению корней системы уравнений

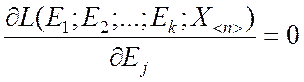                                 ,  .    (2.3.4)

Выражения (2.3.4) представляют собой необходимое условие экстремума функции многих переменных, которое заключается в равенстве нулю всех частных производных данной функции.

Решение уравнений (2.3.4) даёт оценки исследуемых параметров, которые называются оценками максимального правдоподобия.

Таким образом, принятие решения в соответствии с принципом максимального правдоподобия заключается в следующем. На основе выборки X_<n> определяются значения функции правдоподобия для всех возможных состояний E_i, . Среди данных состояний выбирается то, которое обеспечивает максимум функции правдоподобия.

2.3.3. Принцип минимальной вероятности ошибки

Рассматриваемый принцип, так же как и предыдущий, применим в тех случаях, когда известен только условный закон распределения результатов наблюдений. Сущность принципа состоит в том, что минимизируется вероятность принятия неправильного решения. Введём следующие определения.

Ошибкой первого рода называется ошибка, представляющая собой принятие решения о том, что исследуемый объект не находится в предполагаемом состоянии, в то время как в действительности он пребывает именно в этом состоянии.

Ошибкой второго рода называется ошибка, представляющая собой принятие решения о том, что исследуемый объект находится в предполагаемом состоянии, в то время как в действительности он пребывает в другом состоянии.

В общем случае правило решения должно быть таким, чтобы обеспечивалась минимально возможная вероятность принятия ошибочных решений. Если бы была известна функция потерь или функция риска, соответствующая каждому из исходов, то задачу поиска решающего правила, минимизирующего вероятность принятия ошибочного решения, можно было бы переформулировать как задачу нахождения решающего правила, минимизирующего вероятность ошибки либо первого, либо второго рода, в зависимости от того, какая из них связана с большими потерями или большим риском.

Так как функция потерь (риска) неизвестна, то задача поиска решающего правила формулируется как задача минимизации суммы вероятностей ошибок первого и второго рода. Метод решения данной задачи рассмотрим для случая, когда исследуемый объект может находиться в одном из двух состояний E₁ или E₂. Пусть наблюдаемая переменная  является скалярной, а кривые условных законов распределения  при условии, что объект может находиться в состоянии E_i, , имеют вид, изображённый на рис.2.1.