Теоретические основы параметрических методов обработки экспериментальных данных (Раздел 2 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 4

Теорема Муавра-Лапласа описывает поведение биномиального распределения при больших значениях n, что позволяет значительно упростить вычисления. Расчёты по точной формуле

                                        (2.2.12)

при больших значениях n очень громоздки.

В выражение (2.2.12) входит число сочетаний из n элементов по m:

                                                 ,

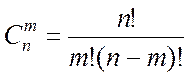где n! = 1×2×…×n,  m! = 1×2×…×m.

П р и м е р 2.2. По линии связи независимо друг от друга передаётся 90 сообщений, каждое из которых состоит из пяти двоичных чисел. Вероятность искажения хотя бы одного числа в сообщении равна 0,06. Определить вероятность того, что число принятых без искажения сообщений будет находиться в интервале [82; 87].

▼ Обозначим через  число неискажённых сообщений при i-й передаче. Эта случайная величина принимает значение ноль с вероятностью 0,06 и единица – с вероятностью 0,94. Следовательно

                                       p_i = p = 0,94;    q_i = q = 0,06.

Обозначим  – общее число неискажённых сообщений. Тогда

                                         ,

.

По формуле (2.2.9) получаем

                    

▲

2.2.3. Неравенство Чебышева

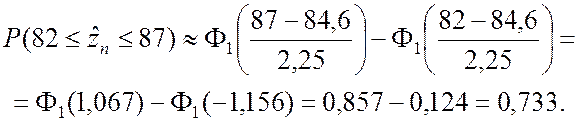
Для любой случайной величины, имеющей конечное математическое ожидание и дисперсию, при каждом  e > 0  имеет место неравенство

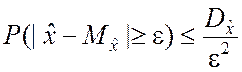                                             .              (2.2.13)

Для противоположного события неравенство Чебышева принимает вид

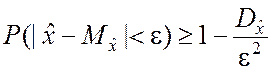                                           .           (2.2.14)

Неравенства (2.2.13) и (2.2.14) можно использовать для получения оценок вероятностей отклонения случайной величины от своего математического  ожидания, если закон распределения случайной величины неизвестен.

П р и м е р 2.3. Найти нижнюю границу вероятности того, что случайная величина , имеющая произвольный закон распределения, отклоняется от своего математического ожидания меньше чем на .

▼ По формуле (2.2.14) получим

                    .

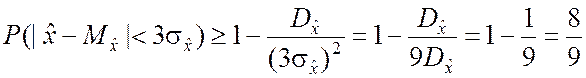Известно, что для нормального закона распределения существует так называемое «правило трёх сигм», согласно которому вероятность попадания случайной величины в  интервал

                                            

близка к единице (» 0,997). Подобное правило существует и для случайных величин, имеющих распределение, отличное от нормального, но при этом вероятность указанного события будет не меньше 8/9.

▲

2.2.4. Теоремы Чебышева и Маркова

Частная теорема Чебышева. При неограниченном увеличении независимых испытаний среднее арифметическое полученных при испытаниях значений случайной величины, имеющей конечную дисперсию, сходится по вероятности к её математическому ожиданию:

                                        .         (2.2.15)

Из (2.2.15) и (2.2.1) следует, что при ограниченном n справедливо приближённое равенство

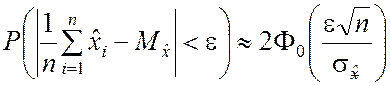                                  ,   (2.2.16)

где 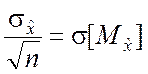 – среднее квадратическое отклонение математического ожидания случайной величины .

В выражении (2.2.16) учтено, что математическое ожидание случайной величины

                                                    

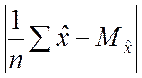
равно нулю.

Применяя неравенство Чебышева (2.2.14) для случайной величины 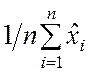, получим

                                      .      (2.2.17)

Формулой (2.2.16) можно пользоваться, когда применима теорема Ляпунова или когда закон распределения каждой случайной величины ,  нормальный. Если же теорема Ляпунова не применима или законы распределения ,  неизвестны, то приходиться определять нижние границы соответствующих вероятностей из соотношения (2.2.17).

При решении практических задач с применением теоремы Чебышева часто возникают трудности, связанные с невозможностью обеспечить независимость испытаний. Теорема Маркова определяет условия, при которых закон больших чисел справедлив и для зависимых испытаний.

Теорема Маркова. Если случайная величина  такова, что

                                                ,

то для любого числа e > 0 существует предельное соотношение