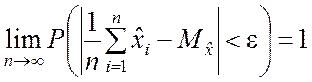Теоретические основы параметрических методов обработки экспериментальных данных (Раздел 2 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 5

                                        .                    

2.2.5. Теорема Бернулли

Если производится n независимых испытаний и вероятность появления события A в каждом из них равна p, то при любом e > 0

                                            ,

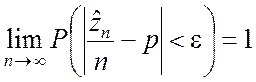где  – число появления события A в n испытаниях.

При n ® ¥ согласно теореме Ляпунова можно считать, что случайная величина

                                                       

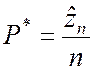
будет иметь нормальное распределение, поэтому справедливо приближённое равенство

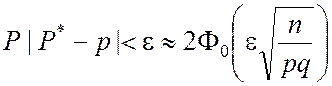                                       .       (2.2.17)

В соотношении (2.2.17) учитывается, что

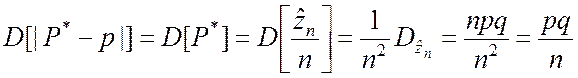  или  .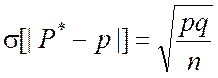

К случайной величине P^* применимо неравенство Чебышева

                                           .                       

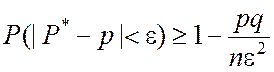Теорема Бернулли устанавливает факт устойчивости частоты, когда вероятность появления события от испытания к испытанию не меняется.

2.3. Элементы теории статистических решений

2.3.1. Задачи принятия статистических решений при обработке экспериментальных данных

Конечной целью обработки экспериментальных данных являются некоторые выводы о состоянии или свойствах исследуемого процесса или объекта. Например, это могут быть выводы о законах распределения случайных величин или параметрах законов распределения, о справедливости каких-либо гипотез и, наконец, выводы о наличии и особенностях взаимосвязей различных показателей, характеризующих свойства объекта. В любом случае из множества возможных выводов необходимо выбрать один, оптимальный в каком-либо смысле. Иначе говоря, необходимо принять решение.

Решением называется некоторое заключение, вывод об исследуемом объекте или его свойствах.

Обработка данных всегда осуществляется в условиях неопределённости, обусловленной неполнотой информации об исследуемом объекте, помехами как естественного, так и искусственного характера. В связи с этим принимаемые решения являются статистическими.

Статистическим решением называется некоторое заключение (вывод) об исследуемом объекте или его свойствах, полученное в результате обработки экспериментальных данных.

Основой для принятия решения является решающее правило(решающая функция), которое служит для выбора из множества возможных решений одного предпочтительного.

Пусть {E}  - множество возможных состояний исследуемого объекта; {X_<n>} – множество возможных результатов наблюдений, а  – множество возможных решений.

Функция

                                                ,

отображающая множество {X_<n>} результатов наблюдений в множество решений , называется решающим правилом (решающей функцией).

Существует много решающих правил, но из этих правил выбирается такое, которое обеспечивает принятие решения требуемого качества, т.е. решения в определённом смысле оптимального.

В связи с этим возникает задача определения оптимального решающего правила. Выбор такого правила определяется рядом факторов:

а) требованиями, которые предъявляются к качеству решения;

б) свойствами экспериментальных данных;

в) условиями, в которых получены данные;

г) дополнительной априорной информацией, которая может быть использована при принятии решения.

Требования к качеству решения определяются потребителем решения (см. рис.1.1) и могут быть сформированы в виде требований минимизации:

-   потерь, которые может понести потребитель при неправильном решении;

-  риска, связанного с принятием неправильного решения;

-  вероятности принятия неправильного решения.

Потерями называются отрицательные последствия, сопровождающие реализацию принятого решения.

Риск – это возможность некоторых потерь со стороны потребителя.

Условия, в которых получены данные, можно разделить на две группы: условия пассивного эксперимента и условия активного эксперимента. В первом случае планирование экспериментальных работ с целью получения данных с необходимыми свойствами отсутствует. Во втором случае эксперимент организуется так, чтобы полученные результаты обладали требуемыми свойствами.