Теоретические основы параметрических методов обработки экспериментальных данных (Раздел 2 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 6

Наиболее важными свойствами совокупности экспериментальных данных, существенно влияющими на качество решающей функции являются объём выборки и её представительность, статистическая устойчивость, однородность, отсутствие аномальных результатов.

Влияние данных свойств на качество решения и вид решающей функции рассмотрено в последующих разделах.

Наиболее важными свойствами априорной информации, оказывающими влияние на формирование решающей функции, являются объём данной информации и её достоверность. Так, в идеальном случае априорная информация I₁ (см. рис.1.1) позволяет получить ряд распределения вероятностей состояний исследуемого объекта, наиболее полной формой информации I₄ является закон распределения вектора результатов наблюдений.

Описание свойств решений может осуществляться с различных позиций. Чаще всего для этого применяется функция потерь.

Пусть множество решений  является дискретным и состоит из l альтернативных решений , . Такими же свойствами пусть обладает и множество {E} состояний объекта, мощность этого множества обозначим через m.

Функцией потерь называется функция p(E_i; ), , , характеризующая последствия принятия решения  при условии, что объект находится в состоянии E_i:

                                                   p(E_i; ) = p_ij.                     (2.3.1)

Функция (2.3.1) записывается в виде матрицы потерь

                                     .

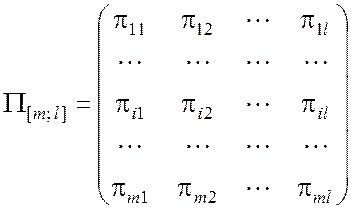Следует заметить, что для определённого состояния E_i исследуемого объекта величина потерь в общем случае будет величиной случайной. В дальнейшем будем полагать, что информация I₆ (рис.1.1) представляет собой сведения о функции потерь (2.3.1).

Учитывая изложенное выше, под объёмом априорной информации будем понимать число видов информации, используемой при формировании решающего правила, а под качеством априорной информации – степень её соответствия объективным свойствам исследуемого объекта.

Оптимальным решающим правилом называется правило, обеспечивающее выполнение требований, предъявляемых к качеству решения в конкретных условиях применения данного правила.

Под условиями принятия решения понимается совокупность перечисленных выше факторов, определяющих выбор правила решения. Обозначим вектор условий, в которых применяется решающее правило R_I(X), символом K_<4>. Компонентами данного вектора являются объём K_X1 и качество K_X2 результатов наблюдений, объём K_I1 и качество K_I2 априорной информации:

                                         K_<4> = (K_Х1,K_Х2, K_I1, K_I2)^т.

С учётом этого решающее правило можно представить в виде функции двух переменных – результатов наблюдений и априорной информации, т.е.

                                                R_I(X) = R(X _<n>; I),

а качество (оптимальность) данного правила применительно к условиям K_<4> охарактеризовать показателем

                                                   L = f(R; K_<4>),

представляющим собой эффект, который достигается в результате использования решающего правила R в условиях K_<4>. Конкретное выражение показателя L при решении различных задач обработки может быть различным. Поэтому оптимальным решающим правилом R₀ для некоторой совокупности условий обработки K_<4>j, , целесообразно считать правило, обеспечивающее экстремум показателя L в условиях K_<4>j:

                                 ,

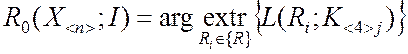где {R} – множество решающих правил.

На практике подбор оптимального решающего правила для некоторых условий обработки выполняется на основе принципов принятия решений. В настоящее время сформулирован ряд таких принципов, основными из которых являются принцип максимального правдоподобия и принцип минимальной вероятности ошибки.

Рассмотрим их более подробно.

2.3.2. Принцип максимального правдоподобия

Данный принцип используется в тех случаях, когда известен только условный закон распределения результатов наблюдений относительно состояния E исследуемого объекта.