Теоретические основы параметрических методов обработки экспериментальных данных (Раздел 2 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 3

где z принимает значение a или b. Это требование вызвано тем, что за пределами интервала

                                          

могут быть существенные ошибки.

П р и м е р 2.1. При обработке информации требуется сложить 1000 чисел, каждое из которых округлено с точностью до 0,01. Полагая, что ошибки округления подчинены равномерному закону распределения, найти вероятность того, что суммарная ошибка округления не превысит 0,2.

▼ Обозначим через ,  ошибку округления i-го числа, а через  – суммарную ошибку округления (n = 1000).

Далее учитываем, что случайная величина, равномерно распределённая на интервале [a; b] имеет математическое ожидание и дисперсию, которые определяются по формулам

                                        ,  .

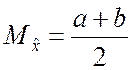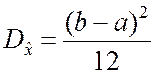Ошибки округления в данном случае распределены на интервале

                                           [a; b] = [–0,005;  0,005],

следовательно,

    ,   .

                       ;   ;

                                   .

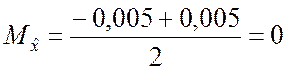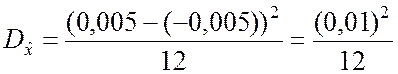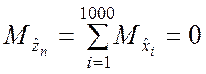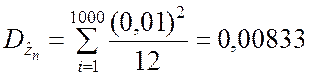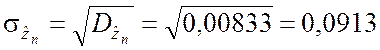Условие (2.2.5) соблюдается, поэтому

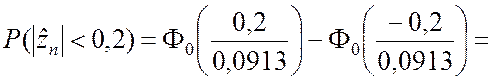
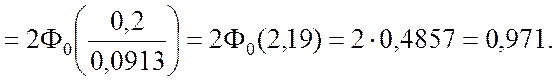
Последнее равенство вытекает непосредственно из формулы (2.2.1), в нём учтено, что функция  Ф₀(x)  является нечётной.

                                                                                                            ▲

2.2.2. Теорема Муавра-Лапласа 

Пусть производится n независимых испытаний, в каждом из которых событие A может появляться с одной и той же вероятностью. Тогда случайная величина , представляющая собой число появлений события A в n испытаниях, будет иметь биномиальное распределение [4]. Если число испытаний велико, то и случайная величина принимает большое число возможных значений. Пользоваться такой случайной величиной затруднительно из-за сложности вычислений. Поэтому целесообразно применять теорему Муавра-Лапласа, которая доказывает сходимость последовательности случайных величин, имеющих биномиальное распределение, к нормально распределённой случайной величине.

Теорема. Пусть  число появлений события A в n независимых испытаниях, в каждом из которых вероятность этого события равна p. Тогда при n ® ¥ имеет место соотношение

                                 

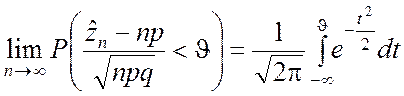
где q = 1– p;  ,  – соответственно математическое ожидание и дисперсия  биномиально  распределённой случайной величины.

Таким образом, нормированная случайная величина

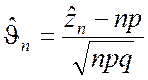                                                                           (2.2.6)

согласно теореме Муавра-Лапласа в пределе будет подчиняться нормированному нормальному закону распределения. Отсюда вытекает приближённое равенство, справедливое при больших значениях n:

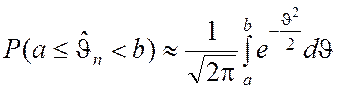                                      .         (2.2.7)

Найдём вероятность попадания случайной величины  в интервал [m₁; m₂). Для этого подставим граничные точки m₁ и m₂ в формулу (2.2.6):

                                        ;     .

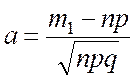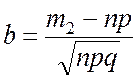Выражение (2.2.7) принимает вид

                                    .                

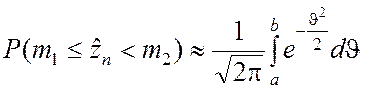Используя табличные функции (2.2.3) и (2.2.4), получаем следующие рабочие формулы:

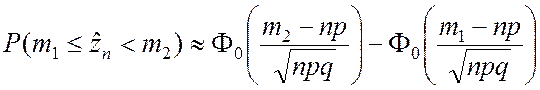                        ;                                                         (2.2.8)  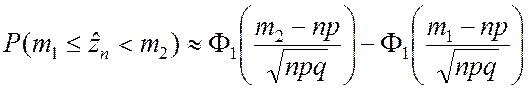                      ;                                                         (2.2.9)

Если n сравнительно мало и разность  |m – np|  соизмерима с 0,5, то не безразлично, относятся ли граничные точки интервала [m₁; m₂) к числу возможных значений  или нет. В этом случае вместо z₁ и z₂ следует брать m₁ – 0,5,  m₂ – 0,5. Тогда соотношения (2.2.8) и (2.2.9) примут вид

          ;                                                        (2.2.10) 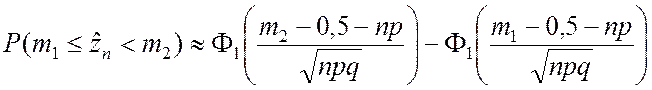            .                                                        (2.2.11)

Следует отметить, что формулы (2.2.10) и (2.2.11) дают более точное приближение, чем (2.2.8) и (2.2.9).

Расчёты по приближённым формулам (2.2.8) – (2.2.11) могут производиться при соблюдении условия

                                                ,

которое непосредственно вытекает из (2.2.5).