Электростатическое поле в вакууме

Лекция 2 Электростатическое поле в вакууме

Сглаженные уравнения для макроскопического поля и потенциала могут быть записаны в нескольких эквивалентных закону Кулона математических формулировках, использование которых определяется спецификой рассмат­ри­ва­емой электростатической задачи. Обсуждаемый в этой лекции  математический фор­ма­лизм находит применение не только в теории электричества, но и в большинстве разделов физики, использующих описание непрерывно изменяющихся величин.

2.1. Поток  и циркуляция векторного поля

В ряде случаев при решении задач электростатики оказывается полезной иная по сравнению с использованной на лекции 1 (но, разумеется, эквивалентная ей по сути)  математическая форма записи закона Кулона. Прежде, чем переходить к ее рассмотрению, необходимо кратко познакомиться с некоторыми новыми математическими идеями, которые весьма полезны не только в электродинамике, но и в других разделах физики, использующих описание величин, непрерывно изменяющихся в пространстве.

В случае, когда в каждой точке пространства R определен некоторый вектор K(R)принято говорить о векторном поле K(R).

Для определения понятия потока N векторного поля K(R) через элемент двумерной поверхности Г₂  удобно ввести понятие вектора элемента площади, определив его длину равной площади рассматриваемого элемента поверхности и задав направление по нормали к этому элементу. Для получения  однозначного определения направления вектора (рис.2.1.a) необходимо договориться о том, в каком из двух возможных направлений нормали проводится вектор. В случае замкнутой поверхности Г₂,  вектор площади dS считается направленным  наружу из объема, ограниченного этой поверхностью. Если же поверхность Г₂ незамкнута,  направление нормали согласовывается с направлением обхода границы этой поверхности Г₁  с помощью  правила  правой  руки:  если  правая  рука   ориентирована  в  пространстве так, что четыре пальца ее кисти указывают направление обхода границы поверхности, то большой палец показывает направление нормали к этой поверхности.

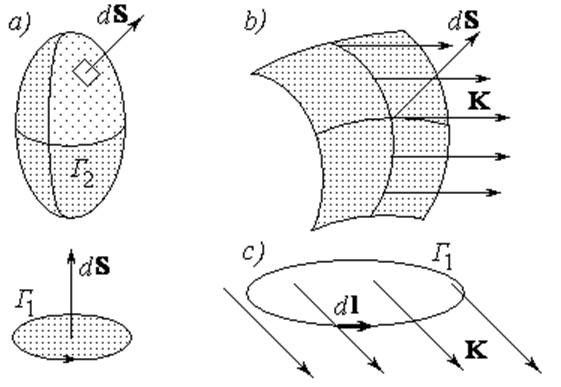
Рис.2.1. Основные интегральные характеристики векторного поля.

a)  – определение направления вектора элемента площади;

b)  – определение потока через элемент поверхности;

c)  – определение циркуляции векторного поля по замкнутому контуру.

Элементарным  потоком векторного поля K(R) через небольшой элемент поверхности  dS  называется скалярное произведение векторов поля и элемента площади (рис. 2.1.b):

                                      .                                 (2.1)

 Полный поток  через замкнутую поверхность, по определению, равен сумме потоков через все ее бесконечно малые элементы и вычисляется с помощью поверхностного интеграла:

                                       .

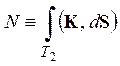 В случае если поверхность замкнута, для поверхностного интеграла используется специальное обозначение:

                                       .

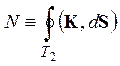Помимо потока удобной интегральной характеристикой векторного поля является его циркуляция С, определяемая суммой по бесконечно малым участкам контура скалярных произведений вектора поля K на элементы длины dl одномерного контура Г₁ (рис.2.1.c):

                                      .

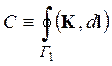Направление вектора dl, согласно определению, выбирается вдоль контура в направлении его обхода.

2.2. Интегральная форма записи уравнений электростатики

Для расчета электростатических полей, создаваемых симметричными распределениями зарядов, часто оказывается полезной теорема Гаусса, утверждающая, что поток вектора напряженности электростатического поля через замкнутую поверхность произвольной формы пропорционален суммарной величине электрического заряда, находящегося внутри этой поверхности. В системе единиц Гаусса эта теорема имеет вид:

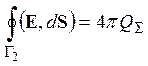                                      .                           (2.2)

Доказательство сформулированного утверждения удобно начать с частного случая элементарного  заряда, помещенного внутрь произвольной замкнутой поверхности, после чего обобщить результат на случай произвольного статического распределения.

Пусть точечный заряд q_k расположен внутри произвольной замкнутой поверхности Г₂ (рис. 2.2.а). Поток вектора напряженности создаваемого им поля через элементарный участок, вырезаемой из поверхности бесконечно малым телесным углом dΩ, согласно определению (2.1), оказывается равным произведению величины заряда на величину этого угла

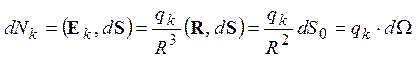.  (2.3)

 и не зависит от расстояния от заряда до поверхности. Соотношение (2.3)  сохраняет свою силу и в случае, если гауссова поверхность имеет более сложную форму (рис. 2.2-б) и пересекает ограниченную телесным углом область несколько раз: