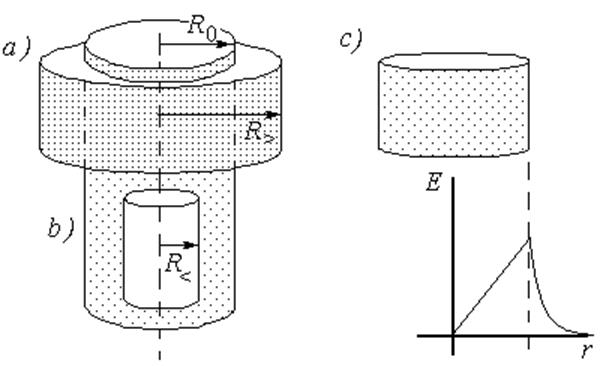
Рис.2.4. Вычисление напряженности электростатического поля бесконечного цилиндра с помощью теоремы Гаусса.
а) – вид гауссовой коробочки
в) – результат расчета напряженности поля бесконечного равномерно заряженного цилиндра.
Поскольку в каждой точке боковой поверхности цилиндра электрическое поле направлено перпендикулярно к ней и постоянно по величине (следствие требования неизменности поля при повороте и смещении вдоль оси цилиндра), полный поток равен произведению искомого поля на площадь боковой поверхности:
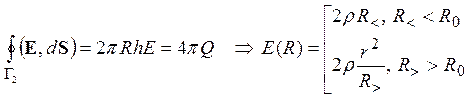
Заряд внутри гауссовой поверхности определяется величиной вырезаемого ею заряженного объема. В результате поле внутри цилиндра линейно возрастает с расстоянием от его оси, а вне него - спадает обратно пропорционально расстоянию.
2.3. Дифференциальная форма записи уравнений электростатики
Наряду с интегральной формой записи уравнений электростатики существует эквивалентная ей дифференциальная форма, которая во многих случаях оказывается более удобной. Пусть электрический заряд непрерывно распределен по некоторому объему. В этом случае теорему Гаусса (2.2) можно применить к физически бесконечно малому объему dV, имеющему форму прямоугольного параллелепипеда:
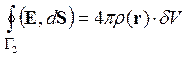(2.5).
Подстановка в формулу (2.5) в соответствии с рис. 2.5.а явных выражений для объема и площадей граней параллелепипеда
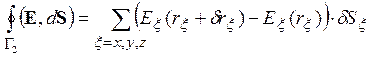
приводит к выражению, содержащему слагаемые, превращающиеся в частные производные при стремлении к нулю размеров выделенного объема
.
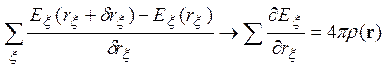Полученное выражение является дифференциальным аналогом теоремы Гаусса. Для его компактной записи в математике вводится специальная операция, называемая дивергенцией, для обозначения которой часто используется обозначение div. Более элегантна и современна другая символическая форма записи этой математической операции - в виде как скалярного произведения оператора пространственного дифференцирования на вектор E:
(2.6)
С точки зрения математики соотношения (2.2) и (2.6) эквивалентны друг другу.
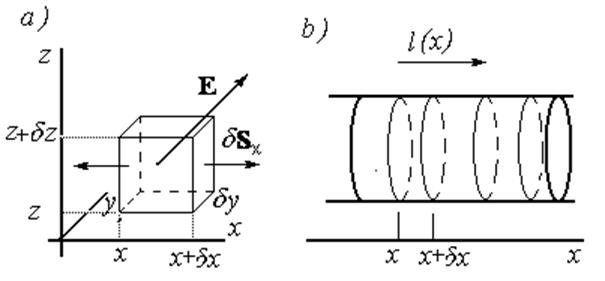
Рис. 2.5. Дифференциальная форма теоремы Гаусса.
а) – обозначения, используемые при выводе соотношения (2.6);
в) – обозначения, используемые при выводе частоты Ленгмюровских колебаний
Интегральной формуле для циркуляции может быть так же сопоставлено дифференциальное соотношение, содержащее специальную операцию вычисления ротора (rot), которую можно определить как результат векторного умножения оператора пространственного дифференцирования на векторную функцию
.
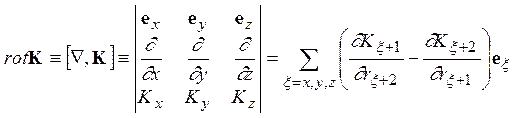В частном случае электростатического поля его ротор тождественно равен нулю. Этот результат можно получить, исходя из интегрального соотношения для циркуляции Е, применяя его к бесконечно-малому замкнутому контуру прямоугольной формы. Однако, использование операторной формы записи позволяет получить этот результат совсем просто, исходя из хорошо известного факта равенства нулю векторного произведения вектора на себя:
Дифференциальные соотношения для электростатического поля можно рассматривать как следствие интегральных уравнений электростатики. Возможен и обратный переход. Так, например, из формулы (2.16) непосредственно следует выражение (2.14) для потока через поверхность бесконечно-малого гауссового объема. Если конечный объем разбить на такие элементарные ячейки, применить к каждой из них это соотношение и учесть, что противоположные потоки через их общие стенки взаимно уничтожаются, в результате суммирования получится интегральная теорема Гаусса (2.8). Разумеется, в курсе математике это утверждение доказывается значительно строже.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.