Электростатическое поле в вакууме, страница 6

Задачи для самостоятельного решения

2.1.         Используя соображения симметрии и теорему Гаусса, рассчитать в произвольной точке пространства элек­трическое поле, создаваемое а) равномерно заряженным по объему шаром, б) равномерно заряженной по поверхности сферой, в) равномерно заряженным по поверхности цилиндром, г) равномерно заряженной по объему бесконечной “толстой плоскостью”. Плотности зарядов и все геометрические размеры считать известными.

2.2. Используя результаты предыдущей задачи рассчитать потенциалы, создаваемые указанными распределениями зарядов и построить графики зависимости напряженности полей и величин потенциалов от расстояния до центра распределения.

2.3.  Рассчитать пространственное распределение электростатического поля, создаваемого атомом водорода в основном состоянии. Ядро атома считать точечным, а плотность заряда в электронном облаке - распределенной сферически симметрично в соответствии с выражением -константа, называемая первым Боровским радиусом.  Указание: нормировочную константу С, входящую в выражение для электронной плотности, вычислить, исходя из того, что полный заряд электронного облака равен заряду электрона.

2.4.  Оценить полную электростатическую энергию атома гелия в основном состоянии, считая, что оба  его s-электрона «размазаны по пространству» в соответствии с выражением для электронной плотности в электронном облаке атома водорода (см. предыдущую задачу). Указание: учесть притяжение электронных облаков к ядру и их взаимное отталкивание.

2.5.  Сильные ядерные взаимодействия удовлетворительно описываются с помощью потенциала, предложенного Юкавой:

                                   .

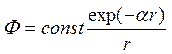Найдите соответствующий такому потенциалу “вектор напряженности ядерных сил”. Как должен быть распределен в пространстве электрический заряд, чтобы создаваемый им потенциал зависел от расстояния так же, как потенциал Юкавы. Получите аналог уравнения Лапласа для случая потенциала Юкавы.

               Указание:  попытайтесь получить более простое выражение для оператора “набла”, справедливого в частном случае, когда он действует на функции

2.5*.Рассчитайте пространственное распределение плотности нейтронов вблизи шарообразного ядерного котла, внутри которого скорость рождения нейтронов постоянна, а поглощения нет. Котел окружен очень толстым слоем вещества, поглощающего нейтроны со скоростью, пропорциональной концентрации частиц. Считать, что внутри и вне котла  поток нейтронов подчиняется уравнению диффузии.

2.6. После прыжка через гиперпространство космический корабль оказался вблизи планеты Гравигаусии, представляющей собой очень длинный однородный цилиндр, вращающийся вокруг своей оси с периодом T. Определите плотность вещества, из которого сложена гравигауссия, если известно, что  на ее поверхности невесомость.

2.7. Оцените, на сколько начнут отставать очень точные часы-ходики, расположенные на поверхности Земли, если точно под ними на глубине 100м прорыть длинный прямой туннель радиусов в 5 м.