Электростатическое поле в вакууме, страница 2

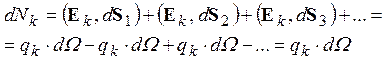
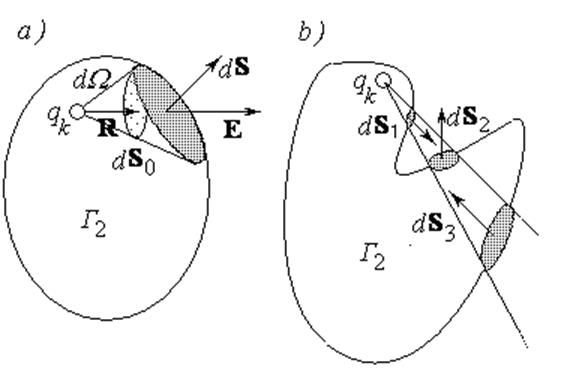
Рис. 2.2. К доказательству теоремы Гаусса для потока электростатического поля.

Интегрирование по телесному углу соотношения (2.3) приводит к результату, соответствующему сформулированной теореме (2.2) для частного случая одного заряда:

                                           .                   (2.4)

Обобщение частного результата (2.4) на случай произвольного числа точечных зарядов является простым следствием принципа суперпозиции и линейности потока по полю:

                              .

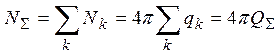Очевидно, что доказанный результат справедлив не только для электростатического, но и для любого центрального поля, пропорционального обратному квадрату расстояния от его точечного источника. Например, аналог рассматриваемой теоремы справедлив в случае классического описания гравитационных полей, что позволяет сводить задачи расчета ускорения свободного падения вблизи массивных тел к аналогичным электростатическим задачам.           

Циркуляция  электростатического  поля по контуру Г₁ имеет смысл работы, совершаемой силами поля по перемещению единичного заряда по замкнутому пути. Из потенциального характера электростатических сил следует, что эта величина тождественно равна нулю:

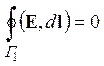.                                    (2.5).

         Совокупность соотношений (2.2) и (2.5) для потока и циркуляции электростатического поля, по сути, эквивалентна ранее выведенным формулам для расчета электростатического поля, создаваемого заданным распределением зарядов и носит название интегральной формы уравнений электростатики. Этот способ записи оказывается наиболее удобным при расчетах полей, создаваемых симметричными распределениями зарядов.

Пример 2.1.  

Электрическое поле  равномерно заряженного цилиндра.

Рассчитать электрическое поле, создаваемое бесконечным цилиндром радиусом R₀, равномерно заряженным объемной плотностью заряда r.

Решение:                         

Заданное распределение зарядов обладает симметрией относительно поворота вокруг оси цилиндра, отражения в любой плоскости, перпендикулярной оси и смещения вдоль оси на произвольное расстояние. Поскольку указанные преобразования не приводят к каким-либо реальным изменениям источников, создаваемое ими поле так же должно оставаться неизменным. Возможные конфигурации поля, обладающие перечисленными свойствами симметрии, приведены на рис. 2.3.

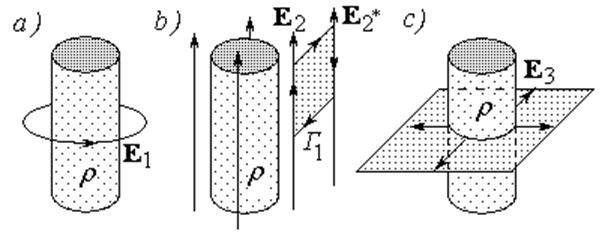
Рис. 2.3.   Допустимые симметрией задачи конфигурации электростатического поля равномерно заряженного цилиндра.

                 E₁ и E₂ – конфигурации реально несуществующих полей;

                 Е₃ – истинная конфигурация электростатического поля.

Вихревое электрическое поле  (рис.2.3.а) невозможно из-за условия потенциальности (2.5):

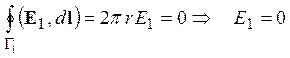
Применение теоремы о циркуляции к контуру типа Г₁ (рис. 2.3.б)  приводит к выводу о независимости величины вектора  напряженности от расстояния:

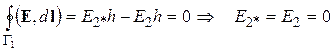
Предположение же о существовании постоянного во всем пространстве электростатического поля, хотя формально и не противоречит уравнениям электродинамики, но традиционно отвергается, как физически абсурдное (по существу сделанное утверждение следует рассматривать как некий дополнительный принцип).

Для расчета напряженности электростатического поля последней конфигурации (рис. 2.3.в) достаточно рассмотреть гауссову поверхность, представляющую собой цилиндр высотой h, ось которого совпадает с осью заданного заряженного цилиндра (рис.2.4.).

Из соображений симметрии ясно, что вектор напряженности электростатического поля в каждой точке пространства должен быть направлен перпендикулярно оси цилиндра (в противном случае отражение в перпендикулярной оси плоскости приведет к изменению конфигурации поля). Т.о.  ненулевым оказывается только вклад в поток через боковую часть цилиндрической гауссовой поверхности.