Электродинамика медленных процессов в плазме. Ионно-звуковые волны. Магнитная гидродинамика

14 Электродинамика медленных процессов в плазме. Ионно – звуковые волны. Магнитная гидродинамика. Ионно-звуковые волны. Основные положения магнитной гидродинамики.(МГД). Обобщенный закон Ома для медленных нерелятивистских процессов. Уравнения динамики плазмы. Условия применимости уравнений МГД. Дисперсионные свойства, полярные диаграммы фазовых скоростей МГД волн. Групповые скорости МГД волн. Использование МГД эффектов для прикладных целей. МГД генератор.

14.1 Ионно-звуковые волны. Ионы очень слабо влияют на высокочастотные волновые процессы в плазме благодаря большому отличию масс электронов и ионов. Однако, влияние ионов чрезвычайно существенно для низкочастотных волн. Сейчас рассмотрим одну из таких ситуаций. Пусть имеется сильная неизотермичность изотропной плазмы. Равновесное максвелловское распределение устанавливается в газе в результате столкновений между частицами. В плазме с малой частотой столкновений время свободного пробега частиц очень велико и она может долго находиться в неравновесном состоянии. Особенно долго может сохраняться двухтемпературное состояние. Распределения электронов и ионов при этом максвелловские, но температура электронов  не равна температуре ионов . В экспериментах очень часто выполняется неравенство >>, Это связано с тем, что при многих методах нагрева плазмы первоначально нагреваются электроны, а затем энергия постепенно передается от электронов к ионам. Законы сохранения энергии и импульса при упругих столкновениях показывают, что обмен энергиями между частицами одного сорта происходит в 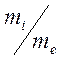 раз быстрее, чем обмен энергиями между электронами и ионами. Поэтому быстрее всего устанавливается максвелловское распределение в каждой из компонент (электронной и ионной) порознь. После этого происходит медленное выравнивание температур. Рассмотрим сейчас двухкомпонентную плазму, в которой выполнено условие >> и будем интересоваться медленным (низкочастотным) процессом, в котором упорядоченные скорости электронов и ионов одного порядка малости (в высокочастотных процессах упорядоченная скорость электронов гораздо больше, чем скорость ионов, допустимо использования приближения неподвижных ионов). Такие волны впервые были исследованы Ленгмюром и Тонксом (1929 г.). Напишем линеаризованные уравнения движения горячих электронов и холодных ионов (будем интересоваться волнами малой амплитуды):

                                                ,

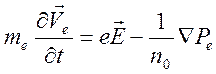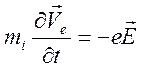                                                .                                               (14.1)

В уравнении движения ионной компоненты отсутствует учет члена , так как . Если просуммировать эти уравнения, то получим

                                                .

Так как  и скорости  и  одного порядка малости в низкочастотных процессах (доказательство этого будет сделано в конце раздела 14.1), то слагаемым 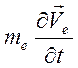 можно пренебречь и написать

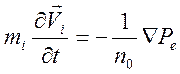                                                .                                         (14.2)

Получился «гибрид»: в левой части уравнения (14.2) стоят величины, относящиеся к ионам, а в правой части стоят величины, относящиеся к электронам. Пренебрежение членом 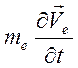 указывает на то, что это можно сделать и в уравнении движения электронов (пренебрежение инерцией электронов):

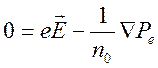                                                .                                             (14.2.А)

Из этого уравнения следует, что электрическое поле потенциально ,

                                                ,            .

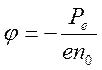Уравнение состояния для давления возьмем в виде

                                                ,

где величины, отмеченные индексом нуль характеризуют однородное стационарное невозмущенное состояние, . Из уравнения (14.2.А) следует

                                                .

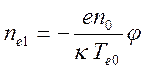Закон Кулона

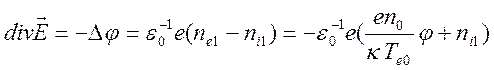
позволяет найти связь

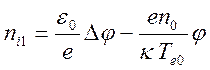                                                .                                    (14.3)

Уравнение движения (14.1) дает возможность получить взаимосвязь между  и

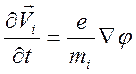                                                .                                                (14.4)

Из (14.3) и (14.4) получаются представления для фурье – образов

                                                ,

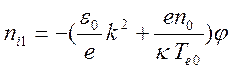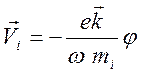                                                .                                               (14.5)

Подстановка этих представлений в уравнение неразрывности                                     

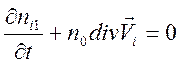
после перехода к фурье – образам дает дисперсионное уравнение

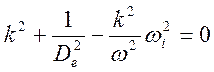                                                ,                                   (14.6)

где 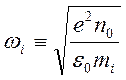 - ионная плазменная частота. Решение уравнения (14.6) можно представить в виде

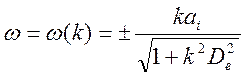                                    , либо ,

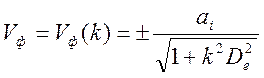где 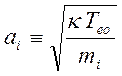 - скорость ионного звука, она определяется температурой электронов  массой ионов. Отметим некоторые дисперсионные свойства: