При этом уравнение движения принимает вид
![]() ,
,
или
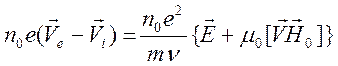 ,
,
или
![]() ,
,
где
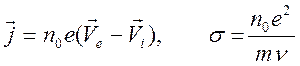 .
.
3). Таким образом, условия применимости магнитной гидродинамики имеют вид
![]()
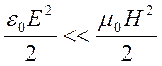
Следует отметить, что при использовании МГД приближения сделаны еще некоторые допущения. Отметим основные из них:
· Допущение о том, что плазма – единый «коллектив» (одна
жидкость), а не многокомпонентная среда. Это приводит к пренебрежению
некоторыми типами волн. Кроме того отсутствует возможность анализа
неизотермической плазмы : ![]() .
.
· Пренебрежение потерями за счет вязкости и теплопроводности.
· Отсутствие учета роли нейтральной компоненты в ситуации частично ионизированной плазмы.
· Пренебрежение кинетическими эффектами.
14.6. Дисперсионные свойства, полярные диаграммы фазовых скоростей МГД волн. Рассмотрим вопрос о дисперсионных свойствах МГД волн малой амплитуды (линейное приближение) на основе системы уравнений
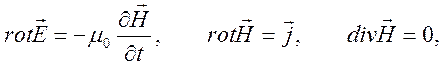
![]() ,
,
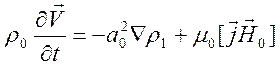 ,
,
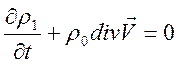 .
.
Ограничимся
случаем ![]() (пренебрежение влиянием омических потерь).
Конечность величины
(пренебрежение влиянием омических потерь).
Конечность величины ![]() обеспечивается при выполнении
соотношения
обеспечивается при выполнении
соотношения
![]() .
.
Эта
система уравнений приводится к одному уравнению для ![]() :
:
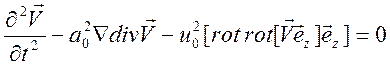 , (14.9)
, (14.9)
где
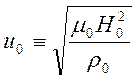 - скорость Альфвена,
- скорость Альфвена, 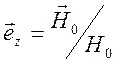 . Используем формулы для плоских
монохроматических полей (для фурье – образов полей)
. Используем формулы для плоских
монохроматических полей (для фурье – образов полей)
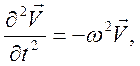
![]() ,
, ![]()
![]() ,
,
![]() ,
,
![]() .
.
С учетом этих формул, уравнение(14.9) приводится к виду
![]() . (14.10)
. (14.10)
Вращением
системы координат вокруг оси ![]() добьемся того, чтобы
вектор
добьемся того, чтобы
вектор ![]() лежал в плоскости
лежал в плоскости ![]() :
:
![]() ,
, 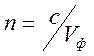 .
.
Проекции
уравнения (14.10) на оси ![]() имеют вид
имеют вид
![]() ,
,
![]() ,
,
![]() .
.
Альфвеновская
волна. Из последней системы уравнений следует, что волна, у которой вектор
скорости направлен вдоль оси ![]() , т.е. перпендикулярен
плоскости распространения (плоскости, содержащей векторы
, т.е. перпендикулярен
плоскости распространения (плоскости, содержащей векторы ![]() и
и ![]() ), такая
волна распространяется независимо от волны с компонентами
), такая
волна распространяется независимо от волны с компонентами ![]() . Фазовая скорость этой альфвеновской волны
имеет вид
. Фазовая скорость этой альфвеновской волны
имеет вид
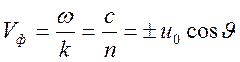 .
.
Вазовая
скорость не зависит от скорости звука ![]() , т.е.
фазовая скорость альфеновской волны одинакова для холодной и горячей плазмы.
Это волна поперечная:
, т.е.
фазовая скорость альфеновской волны одинакова для холодной и горячей плазмы.
Это волна поперечная: ![]() . В ней не происходит возмущения
плотности плазмы.
. В ней не происходит возмущения
плотности плазмы.
Быстрая
и медленная магнитозвуковые волны. Условие существования ненулевых решений
для волн с компонентами ![]() дает биквадратное дисперсионное
уравнение
дает биквадратное дисперсионное
уравнение
![]() .
.
Это уравнение имеет два решения
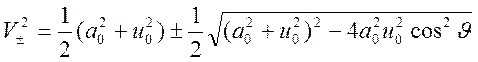 .
.
Или
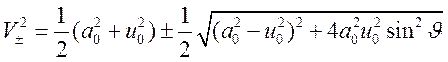 .
.
Знаки
![]() относятся соответственно к быстрой и
медленной магнитозвуковым волнам. Фазовые скорости этих волн зависят не только
от угла
относятся соответственно к быстрой и
медленной магнитозвуковым волнам. Фазовые скорости этих волн зависят не только
от угла ![]() , но и от скорости звука
, но и от скорости звука ![]() . В холодной плазме (
. В холодной плазме (![]() ) распространяется одна быстрая магнитозвуковая
волна с фазовой скоростью
) распространяется одна быстрая магнитозвуковая
волна с фазовой скоростью ![]() . На Рис.14.1 показана
угловая зависимость (полярная диаграмма) скоростей
. На Рис.14.1 показана
угловая зависимость (полярная диаграмма) скоростей ![]() для
случая
для
случая ![]() .
.
В
предельном случае ![]() существует только одна
акустическая волна с фазовой скоростью
существует только одна
акустическая волна с фазовой скоростью ![]() . Такая
ситуация соответствует описанию динамики нейтрального газа.
. Такая
ситуация соответствует описанию динамики нейтрального газа.
14.7.
Групповые скорости МГД волн. Для
одномерного процесса, когда плоская волна распространяется в заданном
направлении ![]() , имеем
, имеем
![]() ,
, 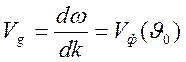 .
.
В
этом частном случае фазовая и групповая скорости МГД волн совпадают. В общем
случае неодномерного процесса ![]() , фазовая и групповая
скорости МГД волн различаются.
, фазовая и групповая
скорости МГД волн различаются.
1). Групповая скорость альфвеновской волны. Из формулы для фазовой скорости получим представление
![]() .
.
Получаем представление для групповой скорости
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.