Электродинамика медленных процессов в плазме. Ионно-звуковые волны. Магнитная гидродинамика, страница 4

где  - энтальпия (тепловая функция) и плотность работы сил давления при изменении объема плазмы,  - работа сил давления,  - учет влияния потока тепла ,  - диссипация за счет электропроводности плазмы. Простейший вид связи  и , .это закон Фурье – Ньютона:

                                                          ,

где  - коэффициент теплопроводности. В случае волн малой амплитуды используется линейное приближение: считается, что  не зависит от . Для описания сильных нелинейных тепловых эффектов учет такой зависимости необходим. Примером может служить эволюция огненного шара при ядерном взрыве.

              5). Уравнение состояния для плотности внутренней энергии

                                                          .

Такое локальное соотношение предполагает отсутствие «релаксации» - задержки во времени при установлении колебательной и вращательной долей энергии. При описании МГД процессов широко используется приближение совершенного газа

                                                          ,

где  - удельная теплоемкость при постоянном удельном объеме .

            В случае пренебрежения диссипацией и при использовании модели совершенного газа будем пользоваться линеаризованной системой уравнений МГД без сторонних источников:

                                             ,

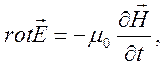
(во втором уравнении сделано пренебрежение током смещения 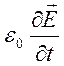, условие такого пренебрежения будет обсуждаться ниже),

                                    ,

                                    ,

                                    ,

                                    ,

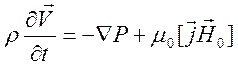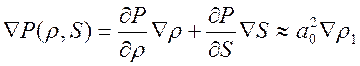где 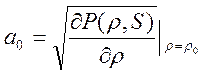 - линейное приближение скорости звука, ,

                                    .

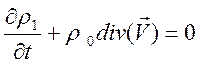14.5. Условия применимости уравнений МГД.

1). Рассмотрение начнем с пренебрежения членом 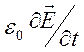 в уравнении Максвелла 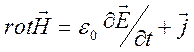. Это можно делать при выполнении любого из неравенств:

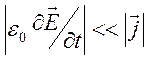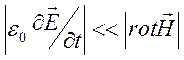            ,          .                            (14.5)

Из закона Ома имеем представление  и первое из неравенств  дает ограничение на длительность временного масштаба  изменения полей

                                                .                                       (14.6)

Из закона электромагнитной индукции Фарадея 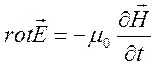 получим соотношение

                                                ,                                        (14.7)

где  - пространственный масштаб изменения полей. Второе из неравенств (14.5) приводится к виду

                                                .                                      (14.8).

При наличии волнового процесса, отношение величин  и  характеризует скорость перемещения возмущений (фазовую скорость ) и неравенство (14.8) принимает вид

                                                .                                                    

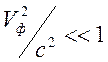Значит, приближение  можно использовать при выполнении (14.6), либо (14.8).

            Второе неравенство в (14.5) приводится к виду 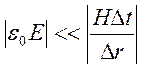. Учитывая представление (14.7) приходим соотношению для плотностей электрической и магнитной энергий

                                                            .

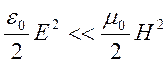            2). При получении Закона Ома использовалось допущение об изотропности:  - скалярная величина. Это допустимо при выполнении условия (обоснование этого условия приводить не будем)

                                                            ,

где  - частота соударений электронов с другими частицами. Дополнительно было использовано допущение о квазинейтральности плазмы

                                                            .

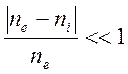В законе Ома имеет место локальная связь между  и  (эта связь алгебраическая, а не дифференциальная). Выясним когда справедливо такое приближение. Напишем линеаризованное уравнение движения электронной компоненты

           .

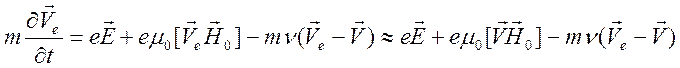Здесь использовано приближение  для медленных процессов. Из этого уравнения движения можно получить закон Ома в алгебраической форме, если пренебречь инерционным членом 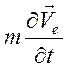 при наличии ограничения

                                                .