где
![]() - электропроводность плазы. Отметим
особенности материальной связи (14.1) в движущейся системе координат:
- электропроводность плазы. Отметим
особенности материальной связи (14.1) в движущейся системе координат:
· линейность,
· локальность (связь алгебраическая),
· изотропность (![]() -
скаляр, а не тензор).
-
скаляр, а не тензор).
Тот
факт, что ![]() - это линейное соотношение и уравнения
Максвелла – линейные, не должно создавать иллюзий, что в магнитной
гидродинамике не будут учтены нелинейные эффекты. Дело в том, что в (14.1)
необходимо сделать преобразование перехода в лабораторную систему координат
(это приведет к нарушению линейности). Для нерелятивистских процессов с
точностью до членов порядка
- это линейное соотношение и уравнения
Максвелла – линейные, не должно создавать иллюзий, что в магнитной
гидродинамике не будут учтены нелинейные эффекты. Дело в том, что в (14.1)
необходимо сделать преобразование перехода в лабораторную систему координат
(это приведет к нарушению линейности). Для нерелятивистских процессов с
точностью до членов порядка ![]() имеем представления
имеем представления
![]() ,
, ![]() ,
, ![]() ,
,
![]() - внешнее магнитное поле (ниже будем
считать
- внешнее магнитное поле (ниже будем
считать ![]() ). Для плотностей токов имеем представления
). Для плотностей токов имеем представления
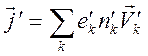 ,
, 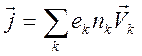 ,
,
где
![]() - заряд, концентрация, скорость
- заряд, концентрация, скорость ![]() - ой компоненты в плазме. С точностью до
членов порядка
- ой компоненты в плазме. С точностью до
членов порядка ![]() имеем представления
имеем представления
![]()
![]() ,
, ![]() ,
,
где
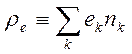 - плотность электрических зарядов. Ниже
ограничимся приближением слабого нарушения электронейтральности:
- плотность электрических зарядов. Ниже
ограничимся приближением слабого нарушения электронейтральности: ![]() и получим обобщенный закон Ома для
медленных процессов в плазме
и получим обобщенный закон Ома для
медленных процессов в плазме
![]() . (14.2)
. (14.2)
Выясним
к каким ограничением приводит, использованное неравенство ![]() . С этой целью сделаем оценку полей,
считая, что плазма состоит из электронов и положительных ионов
. С этой целью сделаем оценку полей,
считая, что плазма состоит из электронов и положительных ионов
![]() ,
, ![]() .
.
Это приводит к неравенству, характеризующему слабое нарушение электонейтральности плазмы
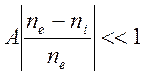 ,
,
где
параметр 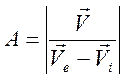 в медленных процессах является величиной
порядка единицы.
в медленных процессах является величиной
порядка единицы.
Закон
Ома (14.2) содержит произведение неизвестных функций ![]() .
Тем самым, здесь имеет место учет нелинейности. Тот факт, что в закон Ома вошла
новая неизвестная функция
.
Тем самым, здесь имеет место учет нелинейности. Тот факт, что в закон Ома вошла
новая неизвестная функция ![]() (упорядоченная скорость
плазмы), делает систему уравнений Максвелла совместно с законом Ома незамкнутой
системой уравнений. Возникает необходимость введения в рассмотрение
дополнительных уравнений, содержащих
(упорядоченная скорость
плазмы), делает систему уравнений Максвелла совместно с законом Ома незамкнутой
системой уравнений. Возникает необходимость введения в рассмотрение
дополнительных уравнений, содержащих ![]() (это будут уравнения
динамики плазмы).
(это будут уравнения
динамики плазмы).
14.4. Уравнения динамики плазмы. Перейдем к дальнейшему замыканию системы уравнений магнитной гидродинамики, привлекая уравнения динамики плазмы. Как уже отмечалось выше, плазму будем рассматривать как единый «коллектив», не различая отдельные компоненты.
1). Уравнение движения плазмы
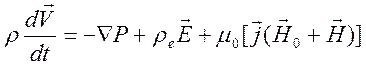 , (14.3)
, (14.3)
где
![]() - плотность и скорость плазмы,
- плотность и скорость плазмы, 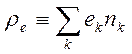 - плотность электрических зарядов,
- плотность электрических зарядов, 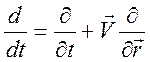 . В уравнении (14.3) нет слагаемого,
учитывающего упругие соударения между частицами плазмы, так как такие
соударения не приводят к изменению полного импульса системы. В результате
соударений происходит обмен импульсами между отдельными частицами и различными
компонентами плазмы. В уравнении движения (14.3) не учитывается диссипация за
счет влияния вязкости. Нелинейность содержится в левой части (14.3) и в членах
. В уравнении (14.3) нет слагаемого,
учитывающего упругие соударения между частицами плазмы, так как такие
соударения не приводят к изменению полного импульса системы. В результате
соударений происходит обмен импульсами между отдельными частицами и различными
компонентами плазмы. В уравнении движения (14.3) не учитывается диссипация за
счет влияния вязкости. Нелинейность содержится в левой части (14.3) и в членах ![]() правой части. В уравнение движения входят
две новые неизвестные функции
правой части. В уравнение движения входят
две новые неизвестные функции ![]() и
и ![]() . Необходимо добавить дополнительные
уравнения для описания этих функций (уравнение неразрывности и уравнение
состояния).
. Необходимо добавить дополнительные
уравнения для описания этих функций (уравнение неразрывности и уравнение
состояния).
2). Уравнение неразрывности (закон сохранения массы) можно использовать в двух эквивалентных формах
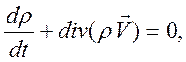
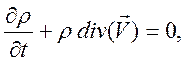 (14.4)
(14.4)
отметим наличие нелинейности в (14.4).
3).
Уравнение состояния для давления ![]()
![]() , либо
, либо ![]() ,
,
где
![]() - температура и энтропия. Простейшим видом
уравнения состояния (его обычно используют в магнитной гидродинамике) является
уравнение состояния совершенного газа
- температура и энтропия. Простейшим видом
уравнения состояния (его обычно используют в магнитной гидродинамике) является
уравнение состояния совершенного газа
![]() ,
,
где
![]() - газовая постоянная.
- газовая постоянная.
4).
Уравнение для плотности внутренней энергии ![]() используем
в виде
используем
в виде
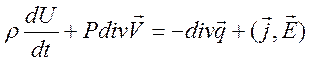 ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.